Soms kan het nuttig zijn om een rooster in te  kleuren  en daardoor te bewijzen dat een bepaalde situatie al dan niet mogelijk is. Deze heuristiek wordt dikwijls gebruikt wanneer je een schaakbord moet opvullen met bepaalde vormen.

Voorbeeld: Kan een 10 x 10 schaakbord opgevuld worden met 25 tetrominos van de vorm 

Oplossing:

• Geef elk vakje van het schaakbord een uniek adres door het rijnummer en kolomnummer van het vakje te noteren. Zo een adres is dan van de vorm .
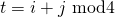• Kleur met de kleur zodat 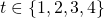. Hierbij is1 = blauw; 2 = geel; 3 = rood; 4 = groen.
  
• Elke tetromino zal door de schikking van de kleuren (cijfers) precies 4 vakjes met vier verschillende kleuren bedekken.
• Aangezien er op het bord 25 keer blauw (1), 26 keer geel (2) 25 keer rood (3) en 24 keer groen (4) voorkomt zal het niet mogelijk zijn om het bord te vullen met 25 tetromino’s