Tag archieven: kleine stelling van fermat

Toepassingen op stelling van Fermat

Geplaatst op door

Nog even in herinnering brengen, de kleine stelling van Fermat luidt: Als p een priemgetal is Ena en p onderling ondeelbaar zijn dan is

    \[a^{p-1}\equiv 1 \mod p\]

 of

    \[a^p \equiv a \mod p\]

 

Nu een paar toepassingen:

  • n^{13}-n is altijd deelbaar door 2730. Bewijs.
    Spoiler


  • 5^p-2*3^p+1 is een p-voud als p priem is. Bewijs. 
    Spoiler



  • 1492^n-1771^n-1863^n+2141^n is steeds deelbaar door 1946. Bewijs dit  en volgende opgaven zelf!
  • n ^2+2n+12 is nooit deelbaar door 112. Tip : vul alle waarden van n in modulo 7.
  • Als n oneven is, dan eindigt de decimale schrijfwijze van 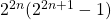2^{2n}(2^{2n+1}-1) steeds op 28.
  • Voor welke n is n^{n+1}+(n+1)^n een drievoud?

            

Stelling van Wilson

Geplaatst op door

De kleine stelling van Fermat zegt ons dat voor een priemgetal p geldt dat a^p \equiv a \mod{p}. Maar dan zijn 1,2, … , p – 1 allemaal nulpunten van de veelterm X^{p-1}-1 in de verzameling \mathbb{Z}_p[X] en dus kunnen we, omdat er geen nuldelers zijn, volgende ontbinding neerschrijven: X^{p-1}-1 = (X-1)(X-2) \cdots (X-(p-1)).
Door hierin X te vervangen door 0, vinden we een deel van volgende stelling:

    \[p \text{ is priem als en slechts als } (p-1)! \equiv -1 \mod{p}\]

Dit resultaat staat bekend als de stelling van Wilson, naar de Engelse wiskundige John Wilson (1741-1793). Nochtans komt dit resultaat een eerste keer voor bij Abu Ali al-Hasan ibn al-Haytham (965-1040)

Bovendien had Wilson geen bewijs van de stelling. Het was Lagrange die in 1771 het eerste bewijs ervan formuleerde.

Het is ook duidelijk dat als n een samengesteld getal is, groter dan 4,  dat  (n-1)! \equiv 0 \mod{n}.

Een algemene vorm is voor ieder oneven priemgetal p en voor ieder positief geheel getal k kleiner dan p:

    \[(k-1)!(p-k)! \equiv (-1)^k \mod{p}\]

Deze veralgemening danken we aan C.F.Gauss

De kleine stelling van Fermat

Geplaatst op door

Als p een priemgetal is en a en p onderling ondeelbaar zijn dan geldt:

    \[a^{p-1} \equiv 1 \text{ mod } p\]

Uit deze stelling, die de kleine stelling van Fermat genoemd wordt en in 1640 een eerste keer vermeld werd, volgt dat voor elke a en voor een priemgetal p geldt dat

    \[a^p \equiv a \text { mod } p\]

De stelling wordt bijvoorbeeld gebruikt om de restklasse modulo een groot getal uit te rekenen. Bereken bijvoorbeeld de rest bij deling van 2^{245} door 11. Volgens de kleine stelling van Fermat is 2^{10} \equiv 1 \text{ mod } 11, dus is 2^{245} \equiv (2^{10})^24.2^5 \equiv 2^5 \equiv 10 \text{ mod } 11.

Er bestaat een veralgemening voor de stelling, die zegt dat als a en m onderling ondeelbaar zijn, geldt

    \[a^{\varphi(m)} \equiv 1 \text { mod }m\]

Hierbij is \varphi(m) de totiënt functie van Euler die het aantal getallen, kleiner dan m, berekent die onderling ondeelbaar zijn met m. Deze stelling wordt de Euler-Fermat stelling genoemd.