Veronderstel dat we n onafhankelijke uitvoeringen doen van eenzelfde Bernoulli experiment met succeskans p. Bij de binomiaalverdeling stellen we ons de vraag hoeveel keer succes hebben we. Nu stellen we volgende vraag: na hoeveel uitvoeringen boeken we voor het eerst succes?
Bijvoorbeeld: hoeveel keer moet de gokker roulette spelen om voor het eerst te winnen?

X is het tijdstip van het eerste succes. X is een stochast met waarden 1,2,…
![Rendered by QuickLaTeX.com \[\text{P(X=k)}=q^{k-1}p\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-858e272ee1cae819dfe4859c11063836_l3.png?media=1678572382)
We zeggen dat X een geometrische verdeling heeft met parameter p. Het is inderdaad een kansverdeling want de som van alle kansen is 1.
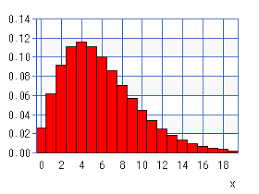
Een voorbeeld van een geometrische verdeling met p=0,10:
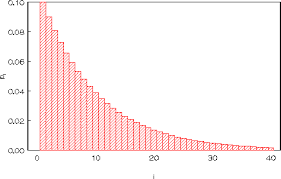
Het gemiddelde van zo een geometrische verdeling is 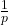 . Een belangrijke eigenschap van de geometrische verdeling is het geheugenverlies: ze vergeet het verleden. Als we weten dat uitvoeringen 1 tot en met i mislukkingen waren, dan heeft de wachttijd vanaf die i-de mislukking tot het eerste succes, juist dezelfde verdeling als de wachttijd vanaf het begin. Met andere woorden de verdeling van die wachttijd tot het eerste succes hangt helemaal niet af van het aantal mislukkingen dat tot dan toe gebeurd is. In symbolen:
. Een belangrijke eigenschap van de geometrische verdeling is het geheugenverlies: ze vergeet het verleden. Als we weten dat uitvoeringen 1 tot en met i mislukkingen waren, dan heeft de wachttijd vanaf die i-de mislukking tot het eerste succes, juist dezelfde verdeling als de wachttijd vanaf het begin. Met andere woorden de verdeling van die wachttijd tot het eerste succes hangt helemaal niet af van het aantal mislukkingen dat tot dan toe gebeurd is. In symbolen:
![Rendered by QuickLaTeX.com \[P(X>i+j|X>i)=P(X>j)\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-57a9cf4fea133963c45f07e147d5975e_l3.png?media=1678572382)
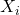 het aantal kaarten in de i-de groep. Dan geldt:
het aantal kaarten in de i-de groep. Dan geldt: ![Rendered by QuickLaTeX.com \[0 \leq X_i \leq 48\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-ba2b507c09a658d2fe2ffcc7084a6ae9_l3.png?media=1678572382)
![Rendered by QuickLaTeX.com \[X_1+X_2+X_3+X_4+X_5=48\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-65cda2951fedf127f5d52d5aa6910813_l3.png?media=1678572382)
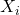 is een kansvariabele en omdat het pak kaarten goed geschud is, zal de kansverdeling van elke
is een kansvariabele en omdat het pak kaarten goed geschud is, zal de kansverdeling van elke 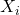 dezelfde zijn.
dezelfde zijn.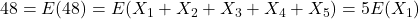 .
.![Rendered by QuickLaTeX.com \[E(X_1)=\frac{48}{5}=9,6\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-50f79ad0e630b542d93d616e003405ab_l3.png?media=1678572382)
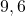 .
.