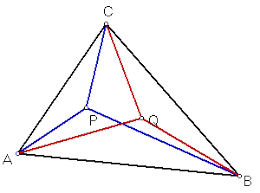
Twee rechten die door het hoekpunt van een hoek gaan en gelijke hoeken vormen met de benen van die hoek, heten isogonaal verwante rechten. In de tekening hierboven zijn de blauwe en rode lijnen in elk hoekpunt isogonaal verwant. De punten P en Q heten isogonaal verwante punten.

Enkele eigenschappen:

• De isogonaal verwante rechten maken ook gelijke hoeken met de deellijn van de gegeven hoek. Ze zijn elkaars spiegelbeeld rond de deellijn.
• Het hoogtepunt van een driehoek en het middelpunt van de omgeschreven cirkel van die driehoek, zijn isogonaal verwante punten.
• Het product van twee zijden van een driehoek is gelijk aan het product van de middellijn van de omgeschreven cirkel met de hoogtelijn, neergelaten op de derde zijde.
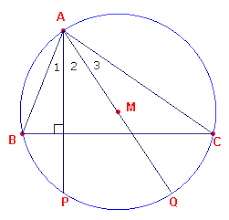
  Immers in driehoek ABS ( S is het voetpunt van de hoogtelijn uit A)  en driehoek ACQ zijn de hoeken in S en Q recht en de hoeken in B en Q zijn gelijk als omtrekshoeken op eenzelfde boog. daardoor zijn de gegeven driehoeken gelijkvormig en uit de evenredigheid van de zijden volgt dan het gestelde.