Om het isogonaal toegevoegd punt van P  te berekenen, construeert men het snijpunt van de spiegelbeelden van AP, BP en CP ten opzichte van de respectievelijke bissectrices van de hoeken A,B en C. Het is duidelijk dat de hoeken CAP en  QAB gelijk zijn. analoog zijn ook ABP en QBC gelijk en BCP en QCA.

Een andere mogelijke constructie werkt met de voetpuntsdriehoek: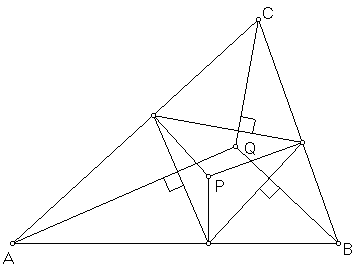

Men tekent de loodlijnen vanuit P op de drie zijden van de driehoek. Hun voetpunten vormen de voetpuntsdriehoek. Construeer nu snijpunt Q van de loodlijnen uit A,B en C op de zijden van de voetpuntsdriehoek. Dan zijn P en Q isogonaal toegevoegd.

Een paar voorbeelden:

• Het middelpunt van de ingeschreven cirkel is isogonaal toegevoegd aan zichzelf.
• Het hoogtepunt van een driehoek en het middelpunt van zijn omgeschreven cirkel zijn isogonaal toegevoegd.