We beschrijven een manier om de waarden van een veelterm ![]() te berekenen als de waarden in opeenvolgende natuurlijke getallen gegeven zijn.
te berekenen als de waarden in opeenvolgende natuurlijke getallen gegeven zijn.
De (eerste) differentie van ![]() is:
is:
![]()
De k-de differentie wordt dan gedefinieerd als:
![]()
Als de graad van ![]() gelijk is aan n, dan formuleren we volgende eigenschappen:
gelijk is aan n, dan formuleren we volgende eigenschappen:
- De graad van
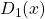 is
is  .
. - De graad van
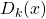 is
is  .
. - Via inductie vinden we
![Rendered by QuickLaTeX.com \[D_k(x)=\sum_{i=0}^k\binom{k}{i}P(x+i)\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-3f5b7917e846a456af91f1b79ca2c842_l3.png?media=1678572382)
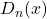 is constant en
is constant en 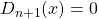 .
.- De waarde van de constante
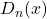 is
is 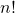 keer de co\”efficiënt\”ent van
keer de co\”efficiënt\”ent van  in
in  .
. 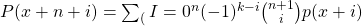 .
.
Veronderstel dat ![]() een veelterm is van graad 2 en dat
een veelterm is van graad 2 en dat ![]() en
en ![]() , bereken dan
, bereken dan ![]() . We zouden een voorschrift voor f kunnen opstellen via interpolatie of door 3 van de gegevens in te vullen in
. We zouden een voorschrift voor f kunnen opstellen via interpolatie of door 3 van de gegevens in te vullen in ![]() en dan het stelsel van 3 vergelijkingen met 3 onbekenden op te lossen. Maar .. laten we eens de differenties berekenen:
en dan het stelsel van 3 vergelijkingen met 3 onbekenden op te lossen. Maar .. laten we eens de differenties berekenen: 
Omdat we weten dat ![]() constant is kunnen we de tabel zelf aanvullen:
constant is kunnen we de tabel zelf aanvullen:
en vinden we dat ![]() .
.
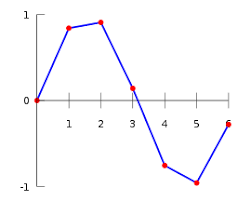
Een ander voorbeeld: zo is er geen veelterm ![]() waarvoor geldt dat
waarvoor geldt dat ![]() voor elke positief natuurlijk getal n. Want :
voor elke positief natuurlijk getal n. Want : ![]() . Dus wordt geen enkele differentie konstant en bestaat er geen veelterm met de gevraagde voorwaarde.
. Dus wordt geen enkele differentie konstant en bestaat er geen veelterm met de gevraagde voorwaarde.


![Rendered by QuickLaTeX.com \[f(n+1)=\sum_{k=0}^n(-1)^{n-k}\frac{(n+1)!}{(k+1)!(n-k)!}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-5f36c4aae7691b7a6e4ddf6bfe1c965b_l3.png?media=1678572382)
![Rendered by QuickLaTeX.com \[f(n+1)=\sum_{l=1}^{n+1}(-1)^{n-l+1}\frac{(n+1)!}{l!(n+1-l)!}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-ab304002d0efcf854047e5f69d66ecb2_l3.png?media=1678572382)