De eerste belangrijke beschaving in het Indus gebied was de Harappa-beschaving rond 2000 voor Christus

Het Vedische volk kwam India rond 1500 voor Christus binnen vanuit wat nu  Iran is.  In deze Vedische beschaving was de bevolking verdeeld in verschillende sociale klassen. de leiding berustte bij de priesterklasse, de Brahmanen. Hun heilige teksten staan bekend staan ​​als de Veda’s. De teksten dateren van ongeveer de 15e tot de 5e eeuw voor Christus en werden gebruikt voor offerrituelen die het belangrijkste kenmerk van de religie waren. De belangrijkste van deze documenten zijn de Baudhayana Sulbasutra geschreven rond 800 voor Christus en de Apastamba Sulbasutra geschreven rond 600 voor Christus. Minder gekend zijn de Manava Sulbasutra geschreven rond 750 voor Christus en de Katyayana Sulbasutra geschreven rond 200 voor Christus.

De Sulbasutra’s zijn bijlagen bij de Veda’s die regels geven voor het bouwen van altaren. Als het rituele offer succesvol zou zijn, moest het altaar zich  zeer precieze afmetingen hebben. Om de goden tevreden te stellen, moest alles met een zeer precieze formule worden uitgevoerd, dus werd wiskundige nauwkeurigheid van het grootste belang geacht. 

Alles wat bekend is van Vedische wiskunde is vervat in de Sulbasutras. Sommige historici beweren dat de wiskunde, meer speciaal de meetkunde, ook moet hebben bestaan ​​als ondersteuning van de astronomie.

Een paar voorbeelden van hun meetkundige kennis:

• Een vierkant dat de som is van twee andere vierkanten
  
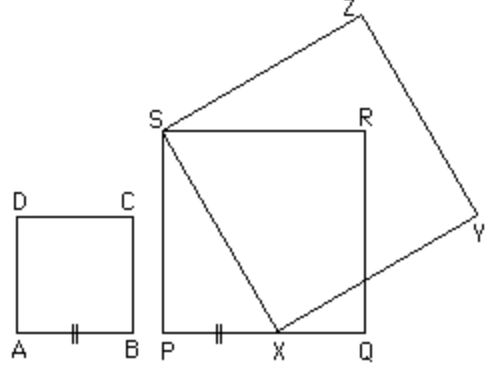
• De diagonaal van een vierkant geeft een vierkant van dubbele oppervlakte.
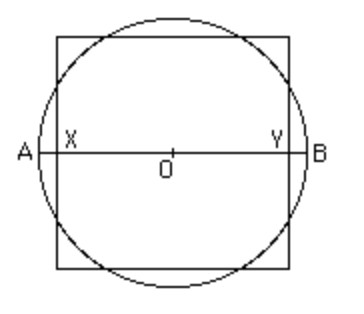
• Een vierkant dat gelijk is aan een cirkel (komt overeen met een waarde voor pi van ongeveer 3,00444)
  
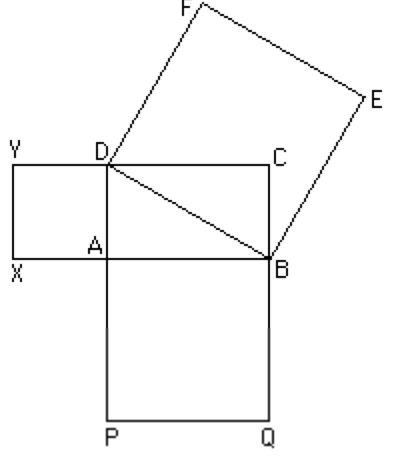
• De som van de oppervlakten van vierkanten van de lengte en breedte van een rechthoek geeft het vierkant van de diagonaal van de rechthoek.
  
• Vermeerder de eenheid met een derde en dit derde met zijn vierde en verminder dat met het 34ste deel van dat vierde. zo bekom je een benadering voor de vierkantswortel van 2: 1,414215

De Sulbasutra’s bevatten geen enkel bewijs van de regels die ze beschrijven. Sommige regels, zoals de methode om een ​​vierkant te construeren dat gelijk is aan een bepaalde rechthoek, zijn exact. Anderen, zoals het construeren van een vierkant gelijk aan dat van een bepaalde cirkel, zijn benaderingen.