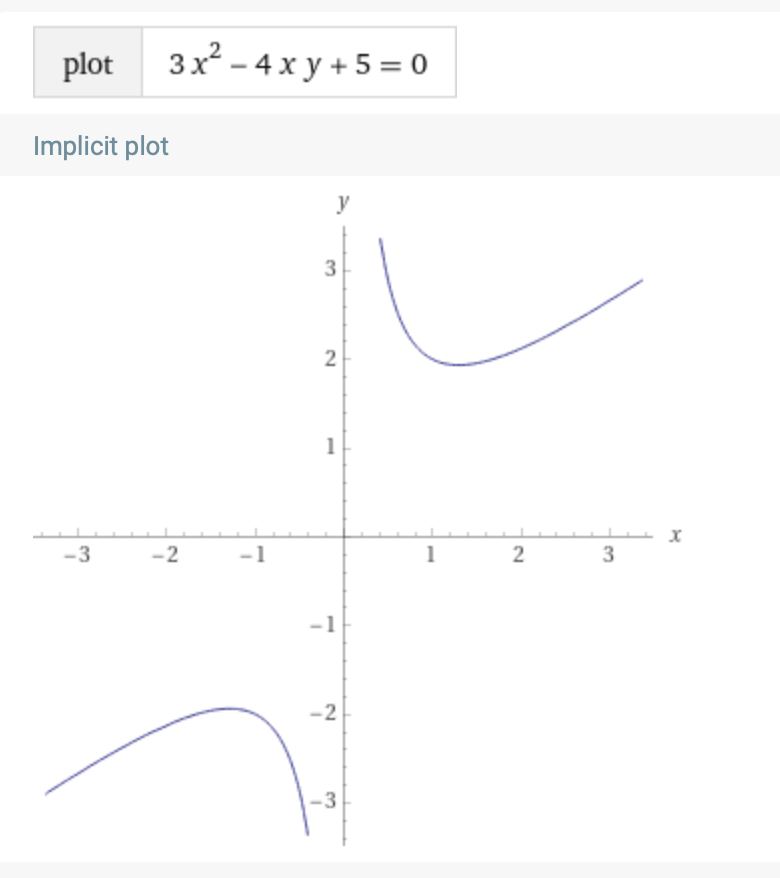
Beschouw de vergelijking
![]()
Bij de vraag naar oplossingen ![]() van deze vergelijking is het nodig te specifiëren tot welke verzameling deze oplossingen moeten behoren. De grafiek, volgens Wolfram Alpha, is:
van deze vergelijking is het nodig te specifiëren tot welke verzameling deze oplossingen moeten behoren. De grafiek, volgens Wolfram Alpha, is:
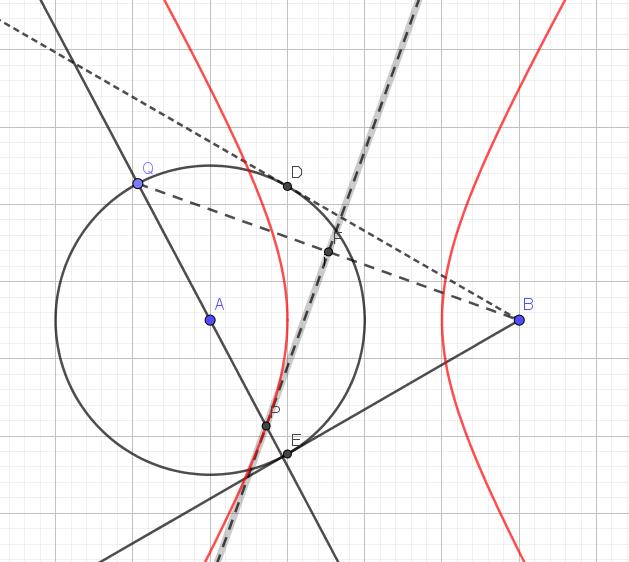
- Elke reële oplossing bepaalt een punt van deze parabool.
- De rationale oplossingen zijn
De hyperbool bevat dus ook oneindig veel punten met rationale coördinaten.![Rendered by QuickLaTeX.com \[\{(q,\frac{3q^2+5}{4q}: q\in \mathbb{Q}\}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-1bb08ca088a7cb8c4c306f574a3209d6_l3.png?media=1678572382)
- Zijn hier gehele oplossingen bij en zo ja dewelke? Als we op zoek zijn naar gehele oplossingen en als de vergelijking ook enkel gehele coëfficiënten heeft, spreken we van een Diophantische vergelijking.
Omdat
moeten, als x en y geheel zijn, zowel![Rendered by QuickLaTeX.com \[3x^2-4xy+5=0\leftrightarrow x(3x-4y)=-5\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-ad4b736fcf97003ec5dd83062c692061_l3.png?media=1678572382)
 als
als  gehele delers zijn van
gehele delers zijn van  . Dit aantal is eindig.
. Dit aantal is eindig.
Dit geeft 4 oplossingen met gehele getallen of met andere woorden 4 roosterpunten op de hyperbool: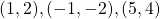 en
en