Tag archieven: hyperbolische meetkunde

Nicolai Lobatschevsky

Geplaatst op door

Wanneer Euclides 23 eeuwen geleden zijn meetkunde in systematische gedaante bracht, had hij zich nooit kunnen inbeelden hoeveel invloed deze later zou hebben. De Euclidische meetkunde is uitermate geschikt om de wereld rondom ons te beschrijven. In de wetenschap voor 1800 heeft men altijd gedacht dat de Euclidische meetkunde het enige meetkundig systeem was.

Onder de axioma’s die Euclides aan de basis van zijn systeem legde, was er één, met name het parallellenpostulaat, dat al vlug in vraag werd gesteld. Men achtte dit axioma van een andere aard als de overige vier en men twijfelde zelfs aan de noodzakelijkheid ervan, omdat het afhankelijk van of een gevolg van de andere axioma’s zou zijn. Gedurende meer dan 2000 jaar hebben beroemde wiskundigen getracht het parallellenpostulaat te bewijzen.

Vanaf de tweede helft van de achttiende eeuw begon men te denken dat men het parallellenpostulaat of elk equivalent postulaat, moest toelaten zonder bewijs. Uiteindelijk leidde dit tot de ontdekking van nieuwe meetkundige systemen. De eersten die hiertoe in staat zijn geweest waren Gauss, Bolyai en Nicolai Ivanovitch Lobatschevsky ( 1792-1856).

Op 23 februari 1826 geeft Lobatschevsky, voor de faculteit wiskunde en natuurkunde van de universiteit van Kazan, een lezing onder de naam Imaginaire meetkunde . Hier zet hij zijn nieuwe ideeën duidelijk naar voor. De essentie van het ongepubliceerde artikel wordt later toegevoegd aan zijn werk De elementen van de meetkunde . Lobatschevsky ondervindt zware tegenwerking en kritiek. Hij herziet zijn werk in een nieuw boek De nieuwe  elementen van de meetkunde. In 1840 verschijnt nog een werk van hem over zijn bedenkingen, namelijk 

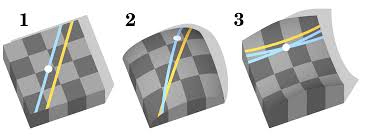
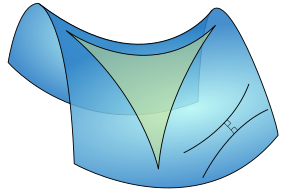
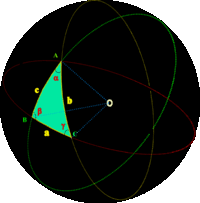
In deze boeken vindt men een nieuwe meetkunde: de hyperbolische meetkunde. Als men het parallellepostulaat ( door elk punt P gaat er juist 1 rechte die een gegeven rechte a niet snijdt)  niet opneemt, dan onderscheidt men twee typen niet-euclidische meetkunde: de hyperbolische meetkunde waar en oneindig veel rechten bestaan door P die a niet snijden en de elliptische meetkunde waar er geen rechte bestaat met die eigenschap.

Om deze meetkunde te visualiseren kan men gebruik maken van het model van Beltrami-Klein of van de modellen van Poincaré.

Niet-Euclidische meetkunde

Geplaatst op door

 

De meetkunde, die we dagelijks gebruiken, wordt Euclidische meetkunde genoemd, ter ere van Euclides, die tussen 330 en 320 voor Christus een aantal boeken, genaamd „Elementen” geschreven heeft.

Hierin wordt  de meetkunde opgebouwd met stellingen vertrekkend van een vijftal postulaten of axioma’s: 
1. Door 2 verschillende punten gaat juist 1 rechte.
2. Een lijnstuk kan naar beide kanten onbeperkt worden
    verlengd.
3. Er kan met elk middelpunt en elke straal een cirkel
    getrokken worden.
4. Alle rechte hoeken zijn gelijk.
5. Door een punt P buiten een rechte , gaat precies één rechte
    die evenwijdig loopt met  de eerste rechte.

Dit laatste axioma staat bekend als het parallellenpostulaat.
Eeuwen heeft men gedacht dat men dit postulaat kon bewijzen aan de hand van de andere vier axioma’s. Trouwens de formulering van het parallellenpostulaat was oorspronkelijk anders.  De gegeven formulering komt van John Playfair. Deze formulering stamt uit 1795 en staat bekend als “Playfair’s axioma” . Een andere gelijkwaardige formulering van dit postulaat is dat de hoekensom van een driehoek gelijk is aan 180°.

Het duurde tot de 19 de eeuw voor het juist inzicht er kwam en wel bij 3 wiskundigen ongeveer gelijktijdig en waarschijnlijk onafhankelijk van elkaar: C.F.Gauss, J.Bolyai en I.Lobatschefsky.

Het was Joha,, Bolyai die tot het inzicht kwam dat het mogelijk was een meetkunde op te stellen, waarin door een punt buiten een rechte oneindig veel rechten gaan die de gegeven rechte niet snijden. Hij publiceerde zijn ideeën in 1832 en gaf zo gestalte aan de hyperbolische meetkunde. De som van de hoeken van een driehoek is hier minder dan 180°.  In de hyperbolische meetkunde wordt dus niet meer aan het parallellenpostulaat voldaan. 
Later werd ook de elliptische meetkunde ontdekt. Elliptische meetkunde is een niet-Euclidische meetkunde, waarbij door een punt buiten een rechte  geen andere rechten bestaat die de gegeven rechte niet snijdt.

De gewone meetkunde is dus niet de meetkunde, maar een  meetkunde. Met andere axioma’s krijgen we een ander soort meetkunde.