Tag archieven: hoogtelijnen

Hoogtedriehoek

Geplaatst op door

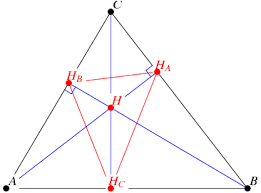
De hoogtedriehoek van een driehoek ABC is de driehoek gevormd door de  voetpunten van de drie hoogtelijnen van deze driehoek.

Enkele speciale eigenschappen:

  • Het hoogtepunt van driehoek ABC is het middelpunt van de ingeschreven cirkel van zijn hoogtedriehoek.
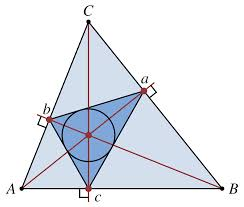
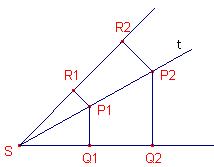
  • Van alle driehoeken ingeschreven in driehoek ABC(d.i de hoekpunten liggen op de zijden  van driehoek ABC) heeft de hoogtedriehoek de kleinste omtrek.
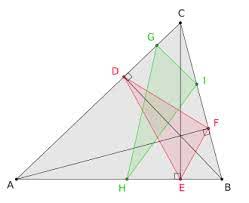    Dit wordt ook wel eens het probleem van Fagnano genoemd naar Giovanni Fagnano die dit probleem stelde in 1775.

Nootje 9

Geplaatst op door

Als de omtrek van een driehoek gelijk is aan 2, bewijs dan dat niet alle hoogtelijnen langer kunnen zijn dan \frac{1}{\sqrt{3}}.

Antwoord

  • Noteer de drie zijden van de driehoek door a,b en c en de hoogtelijnen door h_a,h_b en h_c.
  • Er moet dus minstens 1 hoogtelijn kleiner zijn dan \frac{1}{\sqrt{3}}. De kleinste hoogtelijn staat loodrecht op de grootste zijde.
  • Veronderstel dat a de grootste zijde is dan is a\geq \frac{2}{3}.
  • De oppervlakte van de driehoek is gelijk aan \frac{1}{2}a.h_a, maar ook gelijk aan \sqrt{p(p-a)(p-b)(p-c)}. Hierin is p de halve omtrek en dus is p=1.
  • Bijgevolg is \frac{1}{2}a.h_a = \sqrt{(1-a)(1-b)(1-c)} of  h_a=\frac{2}{a}\sqrt{(1-a)(1-b)(1-c)}\leq 3\sqrt{(1-a)(1-b)(1-c)} .
  • Gebruik nu de ongelijkheid van het meetkundig en rekenkundig gemiddelde : \sqrt[3]{(1-a)(1-b)(1-c)}\leq \frac{1}{3}(1-a+1-b+1-c)=\frac{1}{3}.
  • Hieruit volgt dat \sqrt{(1-a)(1-b)(1-c)} \leq \frac{1}{\sqrt{27}}.
  • Ten slotte is dus h_a \leq 3.\frac{1}{\sqrt{27}}=\frac{1}{\sqrt{3}}.

Hoektransversalen in een driehoek

Geplaatst op door

Neem een driehoek ABC. Een rechte l door een hoekpunt A van de driehoek heet hoektransversaal  of ceviaan van A. We onderzoeken onder welke voorwaarden de hoektransversalen van A,B en C door één punt gaan.

  1. Voor een willekeurig punt P op een hoektransversaal beschouwen we de verhouding van de afstanden tot de twee zijden.
    Omdat \dfrac{P_1R_1|}{|P_1Q_1|}=\dfrac{P_2R_2|}{|P_2Q_2|}, is deze verhouding constant. Noem deze constante v_1 Bij elke transversaal hoort een dergelijke constante. Bereken ze met de klok mee. Nu geldt: De 3 hoektransversalen zijn concurrent als en slechts als v_1v_2v_3=1. Zo geldt bijvoorbeeld voor de binnenbissectrices van een driehoek dat v_1=v_2=v_3=1, dus: de drie binnenbissectrices van een driehoek gaan door één punt.
  2. Laat men ook transversalen toe buiten de driehoek, dan moet men aan de constanten v_i enkel een ander teken geven. Hetr esultaat van hierboven blijft behouden.
  3. We kunnen een hoektransversaal ook kenmerken door de verhouding u_i van de oppervlaktedelen waarin de driehoek door de ceviaan verdeeld wordt.
    U_1=\dfrac{\text{opp} AA'C}{\text{opp} AA'B}=\dfrac{|A'C|}{|A'B|}. Het is eenvoudig te zien dat u_1u_2u_3=v_1v_2v_3 en dus geldt: De 3 hoektransversalen zijn concurrent als en slechts als u_1u_2u_3=1. Onder deze vorm is de stelling ook gekend als de stelling van Ceva.
  4. Nu geldt bijvoorbeeld voor de zwaartelijnen van een driehoek dat u_1=u_2=u_3=1, dus: de drie zwaartelijnen van een driehoek gaan door één punt.
  5. We kunnen dit ook ondzerzoeken voor de drie hooigtelijnen.
    u_1=\dfrac{b \cos \gamma}{c \cos \beta}, u_2=\dfrac{c \cos \alpha}{a \cos \gamma} en u_3=\dfrac{a \cos \beta}{b \cos \alpha} en dus is u_1u_2u_3=1. Bijgevolg geldt: de drie hoogtelijnen van een driehoek gaan door één punt.

De formule van Heroon en gelijkaardige formules.

Geplaatst op door

Misschien kennen jullie de formule van Heroon om de oppervlakte te berekenen van een driehoek in functie van de zijden van de driehoek? Maar kan je deze formule ook uitbreiden naar een formule om de oppervlakte te berekenen van een driehoek in functie van de drie zwaartelijnen of de drie hoogtelijnen? Lees hier de oplossing.
heroon