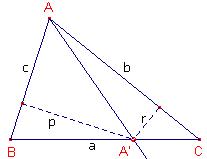
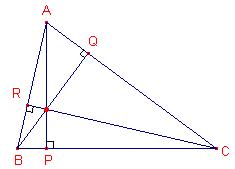
E,F en G zijn de raakpunten van de ingeschreven cirkel aan de zijden van driehoek ABC. Bewijs dat AF,BG en CE door één punt gaan.
Antwoord

Neem een driehoek ABC. Een rechte l door een hoekpunt A van de driehoek heet hoektransversaal of ceviaan van A. We onderzoeken onder welke voorwaarden de hoektransversalen van A,B en C door één punt gaan.
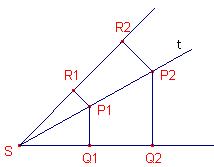 Omdat
Omdat