Tag archieven: herschikkingsongelijkheid

Opgave 2

Geplaatst op door

Bewijs dat voor alle positieve 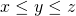x \leq y \leq z geldt dat

    \[\dfrac{x^2}{y+z}+\dfrac{y^2}{x+z}+\dfrac{z^2}{x+y} \geq \dfrac{xy}{y+z}+\dfrac{yz}{x+z}+\dfrac{zx}{x+y }\]

Antwoord

  1. Alsx \leq y \leq z, dan is -z \leq -y \leq -x. Door overal x+y+z op te tellen  vinden we dan dat x+y \leq x+z \leq y+z en \dfrac{1}{y+z}\leq \dfrac{1}{x+z}\leq\dfrac{1}{x+y}.
  2. Door de ongelijkheden x \leq y \leq z en  \dfrac{1}{y+z}\leq \dfrac{1}{x+z} \leq \dfrac{1}{x+y} lid per lid te vermenigvuldigen ( getallen zijn allemaal positief) krijgen we : \dfrac{x}{y+z}\leq \dfrac{y}{x+z} \leq\dfrac{z}{x+y}.
  3. Dan zijn (x,y,z) en (\dfrac{x}{y+z},\dfrac{y}{x+z},\dfrac{z}{x+y})  gelijk geordend.
  4. Gebruik van de herschikkingsongelijkheid geeft de oplossing.

Ongelijkheid van Chebysev of Tsjebysjev

Geplaatst op door

Als we A en B nemen zoals in de herschikkingsongelijkheid, dan geldt

    \[A\geq \frac {(a_1+ \cdots + a_n)(b_1+ \cdots + b_n)}{n} \geq B\]

Immers, als we de termen b_i cyclisch veranderen krijgen we n gemengde sommen: a_1b_1+a_2b_2+ \cdots +a_nb_n,a_1b_2+a_2b_3+ \cdots +a_nb_1, \ldots , a_1b_n+a_2b_1+\cdots+a_nb_{n-1}. Elk van deze sommen ligt volgens de herschikkingsongelijkheid tussen A en B, zo zal hun gemiddelde ook tussen A en B gelegen zijn. Dit gemiddelde is juist de middelste term in de ongelijkheid van Chebychev.

cheby

Voorbeeld:

Voor 2 positieve getallen a,b, geldt: 2(a^5+b^5)\geq (a^3+b^3)(a^2+b^2)

Neem de  de gelijk geordende drietallen (a^2,b^2) en (a^3,b^3). Dan is a^2a^3+b^2b^3 \geq \dfrac{ (a^2+b^2)(a^3+b^3)}{2}. Hieruit volgt het gestelde.

Herschikkingsongelijkheid

Geplaatst op door

De herschikkingsongelijkheid is tezelfdertijd een zeer eenvoudige maar ook een zeer krachtige ongelijkheid. Als a_1\leq a_2\leq \ldots \leq a_n en b_1\leq b_2\leq \ldots \leq b_n dan noemen we (a_1,\ldots,a_n) en (b_1,\ldots,b_n) gelijk geordend en (a_1,\ldots,a_n) en (b_n,\ldots,b_1) omgekeerd geordend.
We noemen A=a_1b_1+\cdots +a_nb_n de geordende som en B=a_1b_n+\cdots +a_nb_1 de omgekeerde som van de gegeven getallen.
Als (x_1,\ldots,x_n) een herschikking (permutatie) is van de getallen (b_1,\ldots,b_n) dan noemen we X=a_1x_1+\cdots +a_nx_n een gemengde som.

De herschikkingsongelijkheid zegt dan:

    \[A\geq X \geq B\]

 

Voorbeeld:

Voor 3 positieve getallen a,b,c geldt: \dfrac{a+b+c}{abc}\leq \dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}

Neem de gelijk geordende drietallen (\dfrac {1}{a},\dfrac {1}{b},\dfrac {1}{c}) en (\dfrac {1}{a},\dfrac {1}{b},\dfrac {1}{c}) . Dan is \dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2} \geq \dfrac{1}{b}.\dfrac{1}{c}+\dfrac{1}{a}.\dfrac{1}{c}+\dfrac{1}{a}.\dfrac{1}{b}=\dfrac{a+b+c}{abc}.