Tag archieven: gulden snede

Een gouden driehoek

Geplaatst op door

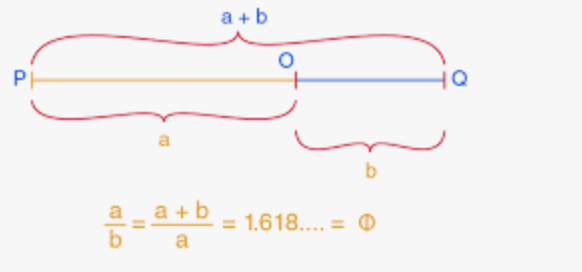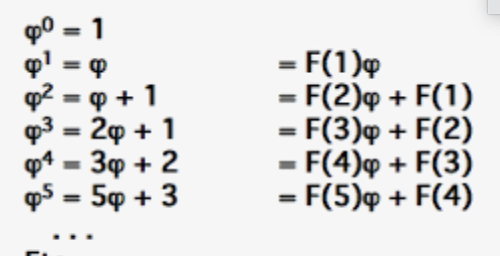
Bij de gulden snede verhoudt het grootste van de twee delen zich tot het kleinste, zoals het gehele lijnstuk zich verhoudt tot het grootste. Geven we het grootste deel aan met a en het kleinste deel met b, dan is de verhouding van beide zo dat 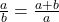\frac{a}{b}=\frac{a+b}{a}. De bedoelde verhouding 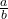\frac{a}{b} noemt men het gulden getal en noteert men met 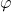\varphi. Het oplossen van de gegeven vergelijking geeft:

    \[\varphi=\frac{1+\sqrt{5}}{2} \approx 1,618\]

Waar kunnen we in een driehoek dit gulden getal zien?

Neem een gelijkbenige driehoek met basishoeken van 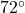72^\circ:

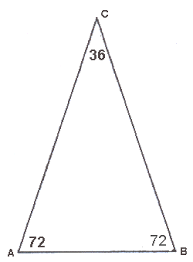
De hoogtelijn uit C verdeelt de overstaande zijde in twee gelijke stukken en de tophoek in twee gelijke hoeken. Zo een halve tophoek meet dan 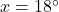x=18^\circ. Dan is 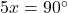5x=90^\circ en 2x=90^\circ-3x. Bijgevolg is \sin 2x=\cos 3x. Gebruiken we nu formules voor de dubbele en drievoudige hoek: 2\sin x\cos x=4\cos^3x-3\cos x.
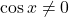Vermits \cos x\neq 0, kunnen we beide leden delen door 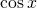\cos x en als we dan de grondformule van de goniometrie toepassen, vinden we

    \[4\sin^2x+2\sin x-1=0\]

Het oplossen van deze vierkantsvergelijking geeft: \sin x =\frac{-1+\sqrt{5}}{4}=\frac{1}{2\varphi}.

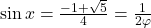
In de bovenstaande driehoek is \sin x=\frac{|AB|}{2|AC|}, dus

    \[\varphi=\frac{|AC|}{|AB|}\]

De gulden snede is dus de lengte van een opstaande zijde van een gelijkbenige driehoek met basishoeken van 72^\circ en basis 1.

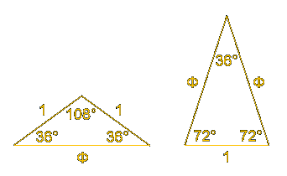
Zoals je in bovenstaande tekening ziet, kan je dit ook verkrijgen met een gelijkbenige driehoek met basishoeken van 36^\circ.

De gulden snede en de rij van Fibonacci

Geplaatst op door

We kennen allemaal de gulden snede. Bij de gulden snede verhoudt het grootste van de twee delen van een lijnstuk zich tot het kleinste, zoals het gehele lijnstuk zich verhoudt tot het grootste. 

Maar er is ook een verband tussen \varphi en de rij van Fibonacci. Noteren we het n-de getal in deze rij door F(n).

  • Als we in bovenstaande uitdrukking \frac{a}{b} vervangen door \varphi, dan vinden we dat \varphi^2=\varphi+1.
  • Maar dat is \varphi^3=\varphi^2+\varphi=2\varphi+1.
  • Dus \varphi^4=2\varphi^2+\varphi=3\varphi+2.
  • Algemeen kan men dan stellen dat :

        \[\varphi^n=F(n)\varphi+F(n-1)\]

Omzetting mijlen naar kilometer

Geplaatst op door

1 mijl( = 1 mi ) is 1,609344 km, wat dicht bij het gulden getal \varphi =1,618 ligt. De waarde van \varphi wordt benaderd door de verhouding van twee opeenvolgende getallen in de rij van Fibonacci. Daarom kan je voor de omzetting van mijlen naar kilometer en omgekeerd gebruik maken van opeenvolgende Fibonacci getallen, met vrij grote nauwkeurigheid.

Sangaku 1

Geplaatst op door

 

Een sangaku is van nature uit een Japanse puzzel uit de Euclidische meetkunde. Vanuit een afbeelding wordt er gevraagd een eigenschap of stelling te herkennen of een berekening uit te voeren. Laten we starten met een eenvoudig voorbeeld:

Antwoord