We kennen het gebruik van een goniometrische substitutie bij het berekenen van onbepaalde integralen. Maar ze kunnen ook hun nut hebben bij de studie van ongelijkheden. Een voorbeeld:
Als a,b,c,en d positieve reële getallen zijn en
![]()
bewijs dan dat ![]() .
.
- Stel
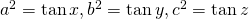 en
en 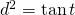
- Omdat
 wordt de gegeven ongelijkheid:
wordt de gegeven ongelijkheid: 
- We gebruiken nu de ongelijkheid van het rekenkundig en meetkundig gemiddelde:

- Analoog
 .
. - Of
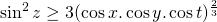 .
. - En
 .
. - Als we nu deze 4 ongelijkheden met elkaar vermenigvuldigen vinden we dat
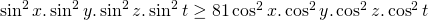 .
. - Hieruit volgt dat
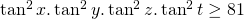 of
of 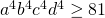 .
. - Omdat a,b,c en d positief zijn volgt hieruit dat
 .
.
