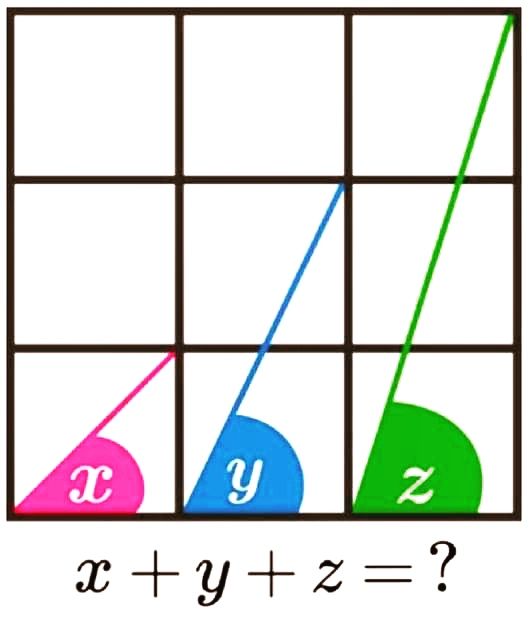
Toon aan dat de som van de breuken ![]() gelijk is aan hun product.
gelijk is aan hun product.
Tag archieven: goniometrie
Nootje 26
Over goniometrie
Het woord goniometrie of trigonometrie komt van twee Griekse woorden: trigonon(driehoek) en metro(maat).
Zo’n 3000 jaar geleden kenden de oude Babyloniërs een vorm van goniometrie en van hen kwam het idee van ![]() . Ze gaven ons zestig minuten in een graad en zestig seconden in een minuut.
. Ze gaven ons zestig minuten in een graad en zestig seconden in een minuut.
Ook de grieken gebruikten al ver gevorderde goniometrie. Euclides en Archimedes ontwikkelden stellingen, weliswaar meetkundig met goniometrische equivalenten. De eerste goniometrische tabel (Tōn en kuklōi eutheiōn (Of Lines Inside a Circle) is waarschijnlijk gemaakt door Hipparchus van Nicaea door sommigen de ‘vader van de goniometrie genoemd.
De tabel was een hulpmiddel bij het oplossen van driehoeken maakte gebruik van koorden en de formule
![]()
De Indiase wiskundige Aryabhata ( 476-550 BC) ontwikkelde de verhoudingen van sinus ( overstaande rechthoekzijde tot schuine zijde) en cosinus ( aanliggende rechthoekzijde tot schuine zijde). In zijn werk Saan ook de oudste bewaard gebleven sinustabellen. 
In de zevende eeuw maakte de Indiase wiskunde Bhaskara een vrij nauwkeurige formule om de sinus van x ( in radialen) uit te rekenen zonder tabel:
![]()
Deze ideeën kwamen via Perzië naar het westen. Al-Khwarizmi maakte in de negende eeuw goniometrische tabellen voor sinus, cosinus en tangens. Een eeuw later gebruikten islamitische wiskundigen de volledige ‘bubbel van 6’ ( sinus, cosinus, tangens, secans, cosecans en cotangens) en zij hadden tabellen voor toenames met een kwart graad, die tot 8 decimalen nauwkeurig waren.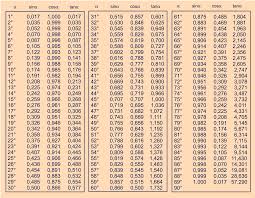
Nu kent de goniometrie vooral toepassingen in de landmeetkunde en de navigatie
Bewijs zonder woorden
We maken gebruik van volgende stellingen:
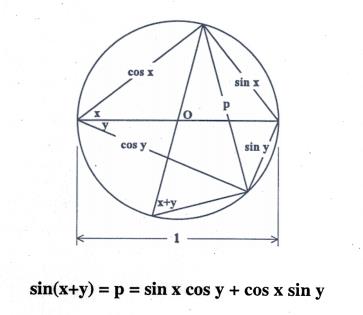
- De sinusregel die zegt dat sin x = 2R .a waarbij a de zijde is tegenover hoek x en waarbij R de straal is van de omgeschreven cirkel. Zo bepalen we in de tekening de zijden met lengte sin x, sin y en
p = sin (x + y). - Een omtrekshoek op een halve cirkel is recht. In combinatie met vorig punt vinden we zo de zijden met lengte cos x en cos y.
- In een koordenvierhoek is de som van de producten van de overstaande zijden gelijk aan het product van de diagonalen. Zo vinden we een uitdrukking voor p.
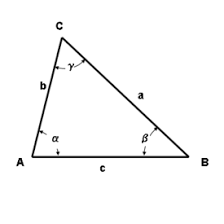
Formules in een driehoek
We geven 7 eigenschappen die, bij het onderzoeken van eigenschappen van een driehoek, zeer nuttig kunnen zijn. Noteer de halve omtrek van de driehoek met s en de oppervlakte met K. Verder zijn r en R respectievelijk de stralen van de ingeschreven en omgeschreven cirkel.
 .
. . (formule van Heroon)
. (formule van Heroon)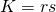 .
. .(sinusregel)
.(sinusregel)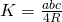 .
. .
.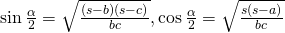 .
.