Tag archieven: getallenraadsel

Een probleem uit getallenleer

Geplaatst op door

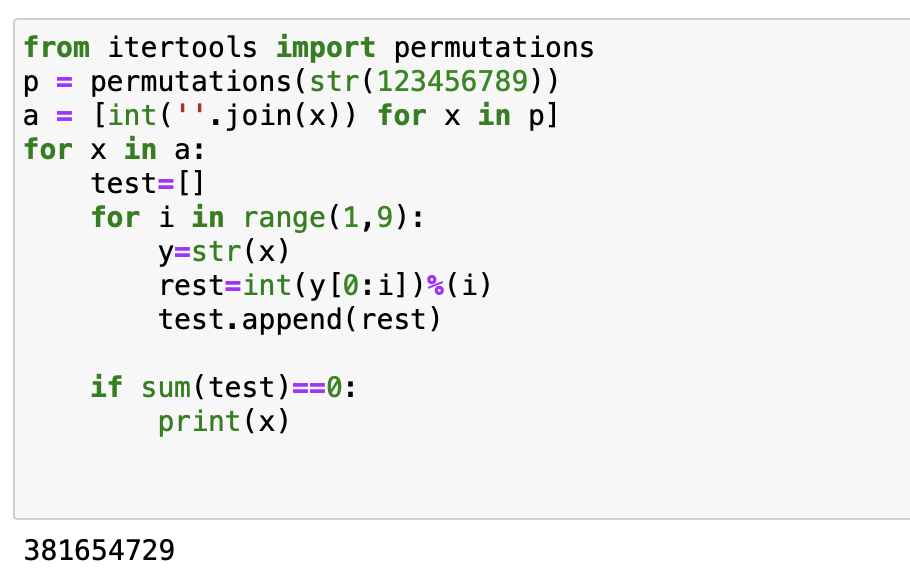
Een natuurlijk getal bestaat uit 9 verschillende cijfers 1 tot en met 9. Schrijft men het opnieuw met telkens de eerste k cijfers, dan is het getal een veelvoud van k. Om welk getal gaat het?

 

  • Het getal gevormd door de eerste 2 cijfers is dus deelbaar door 2, gevormd door de eerste 3 cijfers door 3,…Het getal zelf is dus deelbaar door 9.
  • Dat laatste is altijd voldaan omdat de som der cijfers gelijk is aan 45 en dat is deelbaar door 9. Bijgevolg is het getal zelf ook deelbaar door 9. 
  • We moeten dus enkel controleren voor de eerste 2 tot de eerste 8 cijfers.
  • Het volgende programma in Python geeft de oplossing:

Magische driehoek

Geplaatst op door

Plaats de cijfers van 1 tot en met 9 in de cirkeltjes in het diagram zodat de som van de vier cijfers langs de drie zijden gelijk is aan 17. En hoe kan je ze rangschikken zodat de som langs de drie zijden telkens gelijk is aan 20? Is er een andere som mogelijk? 

Deze puzzel komt uit het boek The Moscow puzzels van Boris Kordemsky(1907-1999), een wiskundedocent uit Moskou.

Spoiler

  • Noteer de som langs de drie zijden door x en de som van de elementen in de hoekpunten door s.
  • de som van alle cijfers 1 tot 9 is 45.
  • Dus 45=3x – s. Hieruit volgt dat s een drievoud moet zijn.
  • Voor x = 17 vinden we s = 6 en krijgen we volgende oplossing:
  • voor x = 20 vinden we s= 15 en vinden we de oplossingen:
  • We vinden ook een oplossing voor x = 21 met s = 18:
  • Andere oplossingen hebben we niet gevonden.