Tag archieven: getallen eigenschappen

Een vierkant vol getallen

Geplaatst op door

\begin{array}{ccc} 1&2&3\\4&5&6\\7&8&9\end{array}

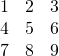
In bovenstaand vierkant zien we dat de som van de elementen op de diagonalen gelijk is : 1+5+9=3+5+7=15. Het is duidelijk dat dit ook geldt voor een 2×2 vierkant met de getallen 1,2,3 en 4:

\begin{array}{cc} 1&2\\3&4\end{array}

De vraag is nu of we dit kunnen veralgemenen: Als we de getallen 1,2,\cdots,n^2 in een nxn rooster plaatsen, in stijgende volgorde, is dan de som van de  elementen op de twee diagonalen dezelfde en zo ja wat is die som?

  • We bekijken eerst welke elementen op de diagonaal staan die links boven vertrekt. Het eerste element is 1 en het volgende staat n + 1 plaatsen verder. Het derde staat weer n + 1 plaatsen verder. Bijgevolg zijn de elementen op die diagonaal van de vorm 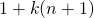1+k(n+1)  waarbij k:0,,2,\cdots, n-1.
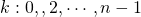  • De som van die elementen is dan S=1+1+(n+1)+1+2.(n+1)+\cdots+1+(n-1)(n+1).
  • Uitgewerkt geeft dit: S=n+\dfrac{(n-1)n}{2}.(n+1)=\dfrac{n^3+n}{2}.
  • Nu de elementen op de andere diagonaal. Het eerste element is n. het volgende ligt één plaats voor 2n, het derde 2 plaatsen voor 3n. De elementen op die diagonaal zijn dus van de vorm :k.n-(k-1) met k:1,2,\cdots,n.
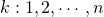  • De som van die elementen is T=n+2n-1+\cdots+n.n-(n-1).
  • Uitgewerkt geeft dit : T=n.\dfrac{n(n+1)}{2}-\dfrac{(n-1)n}{2}=\dfrac{n^3+n}{2}.
  • Hieruit volgt inderdaad dat S=T. We kunnen de eiegenschap dus wel degelijk veralgemenen en de ‘magische’ som van het vierkant is

        \[\dfrac{n^3+n}{2}\]