Neem nu even de bissectrice stelling: de bissectrice van een hoek van een driehoek verdeelt de overstaande zijde in stukken die zich verhouden als de aanliggende zijden. Dit geldt zowel voor de binnen bissectrice als de buiten bissectrice.
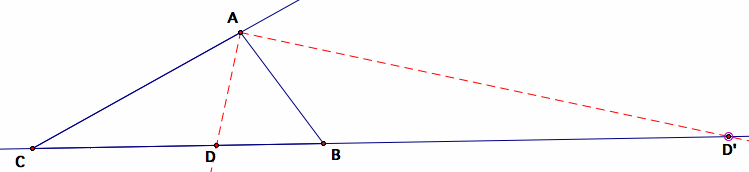
Dus : 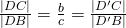 . Als we de lijnstukken een richting geven en tegengesteld gerichte lijnstukken van een tegengesteld teken voorzien, kunnen we hieruit besluiten dat :
. Als we de lijnstukken een richting geven en tegengesteld gerichte lijnstukken van een tegengesteld teken voorzien, kunnen we hieruit besluiten dat :
![Rendered by QuickLaTeX.com \[\frac{|DC|}{|DB|}=-\frac{|D'C|}{|D'B|}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-b01d27fbe18e88d524a685b2a93edc31_l3.png?media=1678572382)
Een viertal punten, dat op een rechte ligt net zoals B,C,D en D’ noemen we een harmonisch puntenviertal. Andere formuleringen:
We hebben dus net bewezen dat de binnen- en buiten bissectrice uit een hoekpunt van een driehoek de overstaande zijlijn snijden in punten die harmonisch toegevoegd zijn ten opzichte van de hoekpunten op die zijlijn.
Als er drie punten op een rechte gegeven zijn, dan kan men een vierde punt construeren zodat ze een harmonisch puntenviertal vormen:
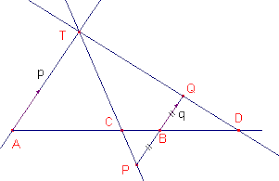
- Gegeven A,B en C.
- Teken door A en B willekeurig twee evenwijdige rechten.
- Teken door C een rechte die de vorige twee rechten snijdt in T en P.
- Verleng PB toto in Q zodat
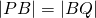 .
.
- Teken TQ en het snijpunt D met AB.
- Dan is
 .
.
Dit volgt uit de gelijkvormigheid van driehoek BDQ met driehoek DAT en de gelijkvormigheid van driehoek BCP en driehoek ACT.
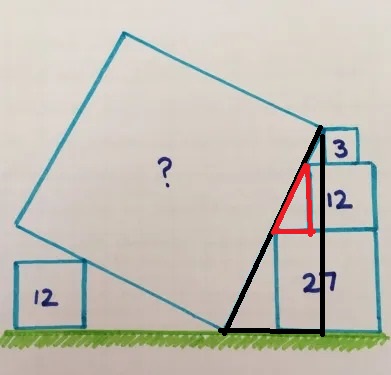
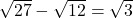 . De andere rechthoekszijde meet
. De andere rechthoekszijde meet  en is dus dubbel zo groot als de horizontale rechthoekzijde.
en is dus dubbel zo groot als de horizontale rechthoekzijde.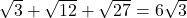 , moet de horizontale rechthoekzijde gelijk zijn aan de helft ervan , dus
, moet de horizontale rechthoekzijde gelijk zijn aan de helft ervan , dus 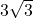 .
.




![Rendered by QuickLaTeX.com \[\begin{vmatrix} a&d&1\\b&e&1\\c&f&1 \end{vmatrix}=0\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-9bacc4787ac3bd07ac10935cf34fb506_l3.png?media=1678572382)

![Rendered by QuickLaTeX.com \[\begin{array}{c} c+x\omega+b\omega^2=0\\b+z\omega+a\omega^2=0\\a+y\omega+c\omega^2=0\end{array}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-2685625ab57bd5d2265d6738c9353aee_l3.png?media=1678572382)
![Rendered by QuickLaTeX.com \[\begin{array}{c} c+x\omega+b\omega^2=0\\a+b\omega+z\omega^2=0\\y+c\omega+a\omega^2=0\end{array}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-a36834b2e74fb31dc30afc310976fd16_l3.png?media=1678572382)