Analyse is het vakgebied dat zich bezighoudt met eigenschappen van functies, zoals extreme waarden, asymptoten, krommen en de door die krommen omsloten oppervlaktes en hellingen van raaklijnen.
De ontwikkeling van de analyse wordt aan Leibniz en Newton toegeschreven, eind 17e eeuw. René Descartes (1596-1650) en Pierre de Fermat (1601-1665) zijn twee Fransen die een enorme bijdrage hebben geleverd aan het ontstaan van de analyse. Ze hebben namelijk, onafhankelijk en ongeveer gelijktijdig, de analytische meetkunde bedacht.
Beiden legden het verband tussen vergelijkingen en krommen van punten die aan die vergelijkingen voldoen, op de inmiddels bekende manier: met coördinaten. Fermat ging altijd uit van een kromme, gegeven door een vergelijking, terwijl Descartes een kromme als een meetkundig object zag, waar hij in sommige gevallen een vergelijking aan kon verbinden.
In deze context willen we graag volgende opgave bekijken:
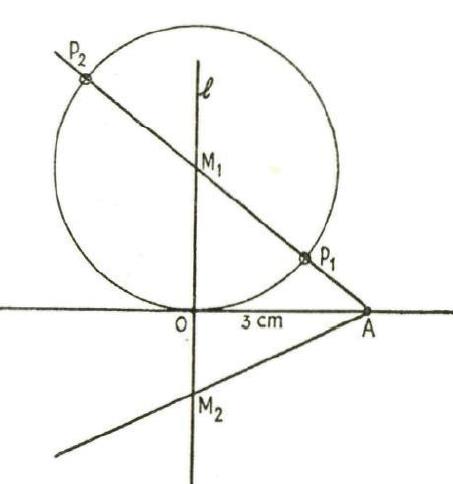
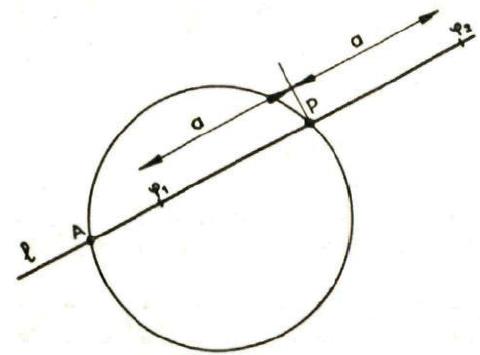
Gegeven is een rechte l en een punt A. Door A worden rechten getrokken, die l snijden. In de figuur ziet men twee van die rechten getekend. Ze snijden l in de punten 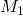
en  . De punten van de strofoïde ontstaan nu op de volgende wijze: Pas op
. De punten van de strofoïde ontstaan nu op de volgende wijze: Pas op  en zijn verlengde de stukken
en zijn verlengde de stukken 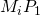 en
en  af beide gelijk aan
af beide gelijk aan  . De strofoïde is de meetkundige plaats van alle punten
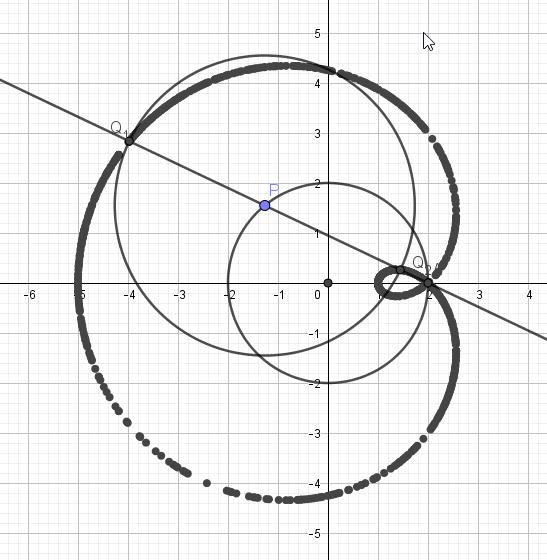
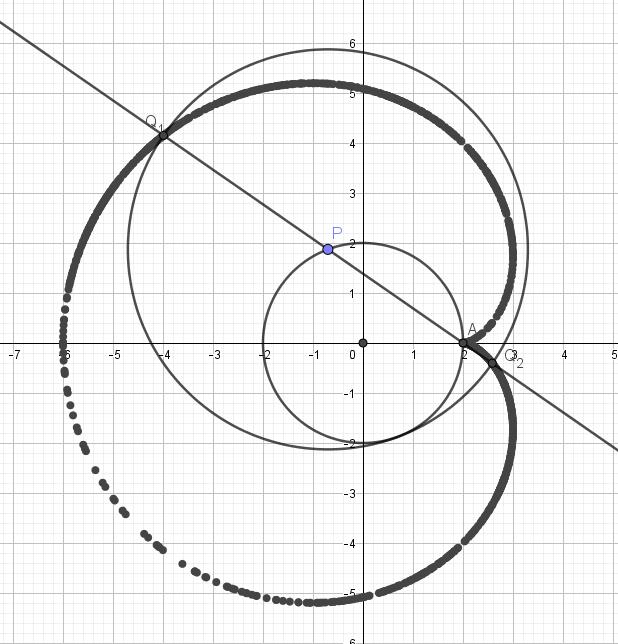
. De strofoïde is de meetkundige plaats van alle punten  die zo geconstrueerd kunnen worden. Met GeoGebra geeft dit :
die zo geconstrueerd kunnen worden. Met GeoGebra geeft dit :
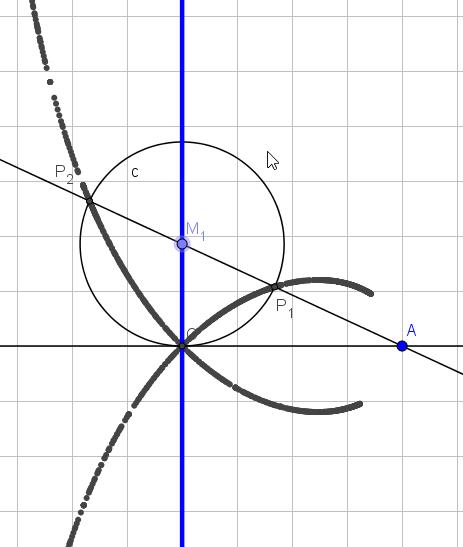
Om de vergelijking te vinden van deze meetkundige plaats nemen we als X-as de rechte OA en als Y-as de rechte l. Het punt A is gegeven door  . Een willekeurige rechte door A heeft als vergelijking
. Een willekeurige rechte door A heeft als vergelijking  . Het snijpunt M heeft dan coördinaten
. Het snijpunt M heeft dan coördinaten 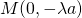 . Uitdrukken dat
. Uitdrukken dat  doen we door te eisen dat
doen we door te eisen dat  .
.
De meetkundige plaats van alle punten P vinden we door 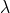 te elimineren uit
te elimineren uit  en
en  . Dit geeft:
. Dit geeft:
![Rendered by QuickLaTeX.com \[y^2=\dfrac{x^2(a-x)}{a+x}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-740b9ae6b891b0a975c036f9b6886eb0_l3.png?media=1678572382)
.
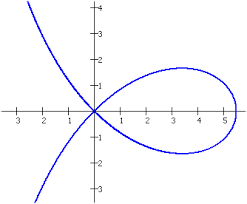
Deze kubische kromme noemt men de strofoïde. We zien ze een eerste keer verschijnen in het werk van Evangelista Torricelli in 1645. In de naam strofoïde herkennen we het griekse ‘strofos’, wat ‘gedraaide band’ betekent. De uitgang ‘oïde’ betekent ‘met de vorm van’. Met andere woorden een strofoïde is een figuur met de vorm van een gedraaide band.
![]() en
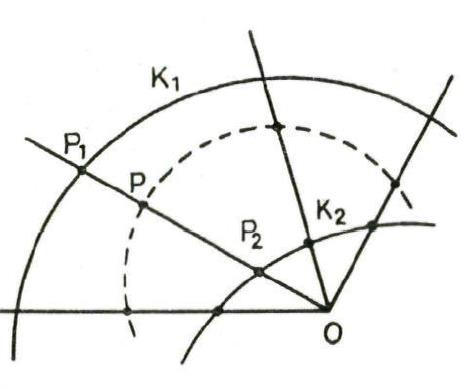
en ![]() en een punt O. Door O trekt men een rechte die
en een punt O. Door O trekt men een rechte die ![]() snijdt in
snijdt in ![]() en
en ![]() in
in ![]() . Op die rechte bepaalt men een punt P zodat
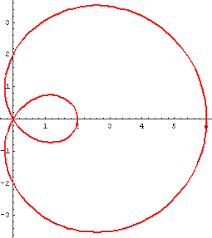
. Op die rechte bepaalt men een punt P zodat ![]() . Wanneer men de rechte nu laat draaien rond O, is de meetkundige plaats van de punten P een cissoïde(afkomstige uit het Grieks: kimos = klimop).
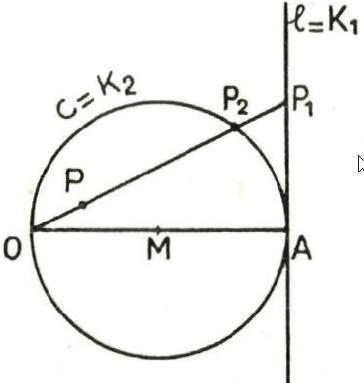
. Wanneer men de rechte nu laat draaien rond O, is de meetkundige plaats van de punten P een cissoïde(afkomstige uit het Grieks: kimos = klimop).![]() een rechte is die raakt in een punt A aan een cirkel (
een rechte is die raakt in een punt A aan een cirkel (![]() ). Voor O neem je het punt op de cirkel diametraal tegenover A.
). Voor O neem je het punt op de cirkel diametraal tegenover A.![]() en de raaklijn heeft als vergelijking
en de raaklijn heeft als vergelijking ![]() . Een willekeurige rechte door O kunnen we voorstellen door
. Een willekeurige rechte door O kunnen we voorstellen door ![]() . Dan is
. Dan is ![]() en
en ![]() . Om de meetkundige plaats te vinden van de punten P, als de rechte rond O draait, moeten we
. Om de meetkundige plaats te vinden van de punten P, als de rechte rond O draait, moeten we ![]() elimineren uit
elimineren uit ![]() en uit
en uit ![]() . Deze laatste voorwaarde bekomen we door de voorwaarde
. Deze laatste voorwaarde bekomen we door de voorwaarde ![]() te projecteren op de X-as. Als resultaat krijgen we
te projecteren op de X-as. Als resultaat krijgen we ![]()