In 1729 schreef Christian Goldbach aan Euler: Kent u de opmerking in het werk van Fermat dat alle getallen 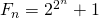 priemgetallen zijn? Hij schrijft dat hij het niet kan bewijzen, en voor zover ik weet heeft ook niemand anders een bewijs kunnen vinden.
priemgetallen zijn? Hij schrijft dat hij het niet kan bewijzen, en voor zover ik weet heeft ook niemand anders een bewijs kunnen vinden.
Fermat had al opgemerkt dat de getallen  priemgetallen zijn voor
priemgetallen zijn voor 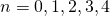 :
:  , vandaar zijn vermoeden. Maar
, vandaar zijn vermoeden. Maar  ging zijn krachten te boven. De getallen
ging zijn krachten te boven. De getallen 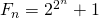 noemt men Fermatgetallen. Euler liet zich echter niet afschrikken en hij kwam tot het verrassende resultaat dat
noemt men Fermatgetallen. Euler liet zich echter niet afschrikken en hij kwam tot het verrassende resultaat dat  geen priemgetal is omdat het deelbaar is door 641. Het vermoeden van Fermat bleek dus niet waar te zijn – een van de zeldzame keren dat Fermat een vermoeden uitsprak dat onjuist is gebleken.
geen priemgetal is omdat het deelbaar is door 641. Het vermoeden van Fermat bleek dus niet waar te zijn – een van de zeldzame keren dat Fermat een vermoeden uitsprak dat onjuist is gebleken.

Waar komt trouwens de vreemde vorm 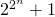 vandaan?
vandaan?
Waarom niet gewoon 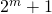 ? Wel, het is eenvoudig te bewijzen dat
? Wel, het is eenvoudig te bewijzen dat 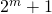 alleen maar een priemgetal kan zijn als m van de vorm
alleen maar een priemgetal kan zijn als m van de vorm 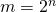 is. Dit komt omdat, als
is. Dit komt omdat, als  oneven is en groter dan 1, dan is
oneven is en groter dan 1, dan is  . Op die manier kan men bewijzen dat m geen oneven deler kan hebben.
. Op die manier kan men bewijzen dat m geen oneven deler kan hebben.
Hoe zit het met  ? Daar lijkt zonder computer geen beginnen aan. Toch lukte het Landry en Le Lasseur in 1880 een volledige ontbinding te vinden. Ook van
? Daar lijkt zonder computer geen beginnen aan. Toch lukte het Landry en Le Lasseur in 1880 een volledige ontbinding te vinden. Ook van 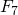 , een getal van 39 cijfers,
, een getal van 39 cijfers, 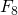 (78 cijfers),
(78 cijfers), 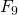 (155 cijfers) en
(155 cijfers) en 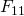 ( 617 cijfers) zijn inmiddels volledige ontbindingen gevonden. Geen van alle zijn het dus priemgetallen. Ook
( 617 cijfers) zijn inmiddels volledige ontbindingen gevonden. Geen van alle zijn het dus priemgetallen. Ook  is geen priemgetal, maar daarvan is alleen maar bekend dat het deelbaar is door 455925777 en 6487031809. Van de resterende factor kennen we de ontbinding niet.
is geen priemgetal, maar daarvan is alleen maar bekend dat het deelbaar is door 455925777 en 6487031809. Van de resterende factor kennen we de ontbinding niet.
Van nog veel meer Fermatgetallen is bewezen dat ze geen priemgetallen zijn. In feite is er nog steeds geen enkele grotere priem dan 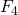 bekend. Bestaat er dus wel een zesde Fermat priemgetal? Het kleinste Fermat getal waarvan we niet weten of het priem is, is
bekend. Bestaat er dus wel een zesde Fermat priemgetal? Het kleinste Fermat getal waarvan we niet weten of het priem is, is  , een getal van 1262612 cijfers. Verder onderzoek ligt nog open…
, een getal van 1262612 cijfers. Verder onderzoek ligt nog open…
![]()
![]()
![]() door 11. Volgens de kleine stelling van Fermat is
door 11. Volgens de kleine stelling van Fermat is ![]() , dus is
, dus is ![]() .
.![]()
![]() de totiënt functie van Euler die het aantal getallen, kleiner dan m, berekent die onderling ondeelbaar zijn met m. Deze stelling wordt de Euler-Fermat stelling genoemd.
de totiënt functie van Euler die het aantal getallen, kleiner dan m, berekent die onderling ondeelbaar zijn met m. Deze stelling wordt de Euler-Fermat stelling genoemd.