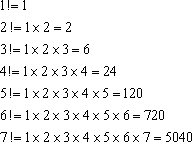Een faculteitsconform getal is een natuurlijk getal dat de som is van de faculteiten van zijn cijfers. Alhoewel 1=1! en 2=2!, noemen we 1 en 2 geen facultietsconforme getallen, omdat er niet sprake is van een som.
Wel een goed voorbeeld is
![]()
We kunnen de gebruikelijke onderzoeksvragen stellen: hoeveel van dergelijke getallen bestaan er? Eindig veel of oneindig? kan je ze genereren met een formule?
Wat we zeker kunnen vaststellen is dat ze maximaal uit 7 cijfers bestaan, want stel n een faculteitsconform getal met n cijfers, dan is
![]()
Er blijkt nog slechts 1 ander faculteitsconform getal te bestaan, namelijk 40585. Dit getal werd in 1964 via computerberekeningen gevonden door Leigh Janes en Ron S. Dougherty.
In de Nederlandse wiskundeliteratuur wordt een faculteitconform getal ook wel geldermangetal genoemd, naar de Nederlandse wiskundige en informaticus Henk-Jan Gelderman.