Bereken de kans dat de determinant van een 3×3 matrix, met natuurlijke getallen als elementen,  oneven is.

• Gegeven een matrix .
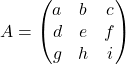• Zijn determinant is

     

• Omdat het gaat over even/oneven kunnen we modulo 2 werken. 
• Determinant oneven betekent dan dat de determinant 1 is en dus dat de matrix inverteerbaar moet zijn.
• Een matrix is inverteerbaar als de kolommen onafhankelijk zijn. Kies de eerste kolom willekeurig ( mag niet 000 zijn) . Dan heb je hiervoor 7 mogelijkheden.
• De tweede kolom mag geen veelvoud zijn van de eerste, maw mag er niet aan gelijk zijn. Dus heb je hiervoor nog 6 mogelijkheden.
• De derde kolom mag niet gelijk zijn aan de eerset of de tweede , maar ook niet gelijk aan de som van die twee ( en natuurlijk ook niet 000). Hiervoor heb je 4 mogelijkheden .
• Er zijn 7x6x4=168 mogelijkheden om determinant 1 te vinden. Er zijn 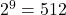mogelijke matrices te vormen met nullen en enen.
• De kans dat een 3×3 matrix met natuurlijke elementen oneven is , is dus