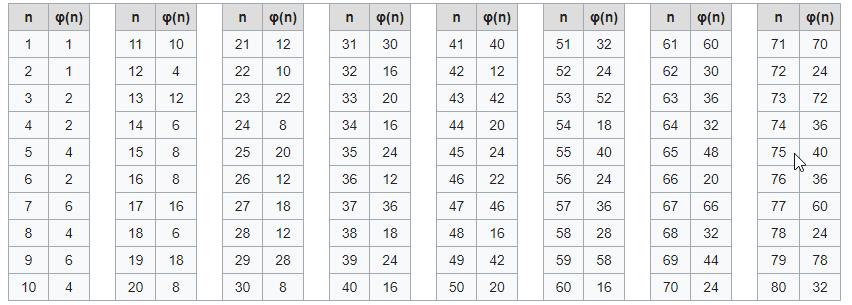
De Euler-phi functie, ook wel totiënt functie of indicator genoemd, telt het aantal positieve natuurlijke getallen kleiner dan of gelijk aan n, die onderling ondeelbaar zijn met n. Notatie: ![]() .
.
Zo is bijvoorbeeld ![]() , want de enige getallen die onderling ondeelbaar zijn met 10 en kleiner zijn dan 10, zijn 1,3,7 en 9.
, want de enige getallen die onderling ondeelbaar zijn met 10 en kleiner zijn dan 10, zijn 1,3,7 en 9.
Enkele eigenschappen:
 .
.- Als p een priemgetal is dan is
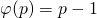 .
. - Als p een priemgetal is dan is
 .
. - Als
 de priemontbinding is van n, dan geldt
de priemontbinding is van n, dan geldt  . Dit kan je ook schrijven als :
. Dit kan je ook schrijven als :
![Rendered by QuickLaTeX.com \[\varphi(n)= n.\prod_{p|n}(1-\frac{1}{p})\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-24440b901b65628156ac10b82cdfdeb2_l3.png?media=1678572382)
Hierbij doorloopt p alle priemdelers van n.

- De indicator geeft ook de omvang aan van de multiplicatieve groep van natuurlijke getallen modulo n