Tag archieven: erdos

Ongelijkheid van Erdös-Mordell

Geplaatst op door

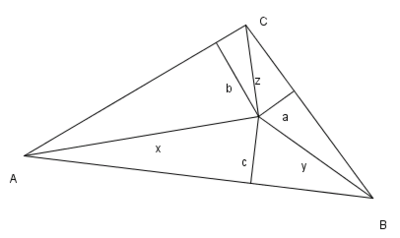
Deze ongelijkheid vertelt ons dat, voor een punt in het inwendige van een driehoek, dat de som van de afstanden tot de hoekpunten niet kleiner is dan het dubbel van de som van de afstanden tot de zijden van de driehoek. Dit werd door Paul Erdös( 1913-1996) als een vermoeden geformuleerd in 1935 en in hetzelfde jaar nog bewezen door de Britse wiskundige Louis Mordell (1888-1972).

    \[x+y+z \geq 2(a+b+c)\]

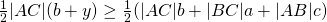  • b+y\geq h_B, dus is \frac{1}{2}|AC|(b+y)\geq\frac{1}{2}(|AC|b+|BC|a+|AB|c). Hieruit volgt dat |AC|y\geq |BC|a+|AB|c.
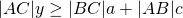  • Door het inwendig punt te spiegelen rond de bissectrice van C, vinden we dat |AC|y\geq |BC|c+|AB|a.
  • Analoge redeneringen geeft ook dat 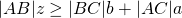|AB|z\geq |BC|b+|AC|a en |BC|x\geq |AC|c+|AB|b.
  • Oplossen naar x,y en z geeft dit 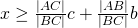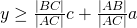x\geq \frac{|AC|}{|BC|}c+\frac{|AB|}{|BC|}b,  y\geq \frac{|BC|}{|AC|}c+\frac{|AB|}{|AC|}a, en z\geq \frac{|BC|}{|AB|}b+\frac{|AC|}{|AB|}a.
  • Lid per lid  optellen van deze ongelijkheden geeft: x+y+z \geq ( \frac{|AC|}{|BC|}+ \frac{|BC|}{|AC|})c+( \frac{|BC|}{|AB|}+ \frac{|AB|}{|BC|})c+( \frac{|AC|}{|AB|}+ \frac{|AB|}{|AC|})b.
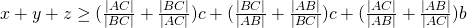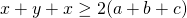  • Uit de ongelijkheid over het rekenkundig en meetkundig gemiddelde volgt dat de coëfficiënten van a,b en c alle groter of gelijk zijn aan 2, zodat x+y+x \geq 2(a+b+c).