Is het mogelijk om een driehoek te verdelen in een willekeurig aantal driehoeken met gelijke oppervlakte?

• Voor n = 2  gebruiken we een zwaartelijn. Driehoeken ACM en ABM hebben een gelijke basis ( CM = MB)  en een zelfde hoogte ( afstand van A tot BC).
  
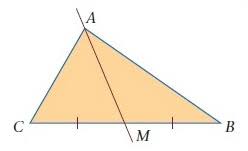
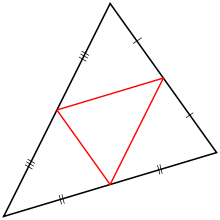
• Voor n = 4 gebruiken we  de constructie van de middenparallel. Hier hebben we 4 congruente driehoeken, dus 4 driehoeken met gelijke oppervlakte.
  
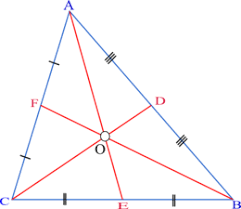
• Voor n = 6 tekenen we de drie zwaartelijnen. Noteren we met S(ABC) de oppervlakte van driehoek ABC. Dan is S(AOD)=S(DOB), S(BOE)=S(COE) en S(FOC)=S(AOF). Maar ook is S(ACE)=S(AEB) of S(AFO)+S(FOC)+S(COE)=S(AOD)+S(ODB)+S(BOE). Na vereenvoudiging volgt hieruit dat S(AOF)=S(AOD). Herhaling met de twee andere zwaartelijnen levert uiteindelijk volgend resutaat: de drie zwaartelijnen verdelen driehoek ABC in zes driehoeken met gelijke oppervlakte.
  
• Voor willekeurige n werken we als volgt. Neem het voorbeeld van n = 5. Als we 5 driehoeken moeten hebben met gelijke oppervlakte, kiezen we een punt P op BC zodat 4.S(ACP)=S(APB). Omdat  deze driehoeken dezelfde hoogte hebben volstaat het P zo te kiezen dat PB= 4. CP. Daarna kiezen we een punt Q op AB zodat 3.S(PAQ)=S(PQB). Analoog voor de consructie van R en S.