Dit artikel is van de hand van Hannah Prause, leerlinge van 6MTWI van het H.Drievuldigheidscollege in Leuven.

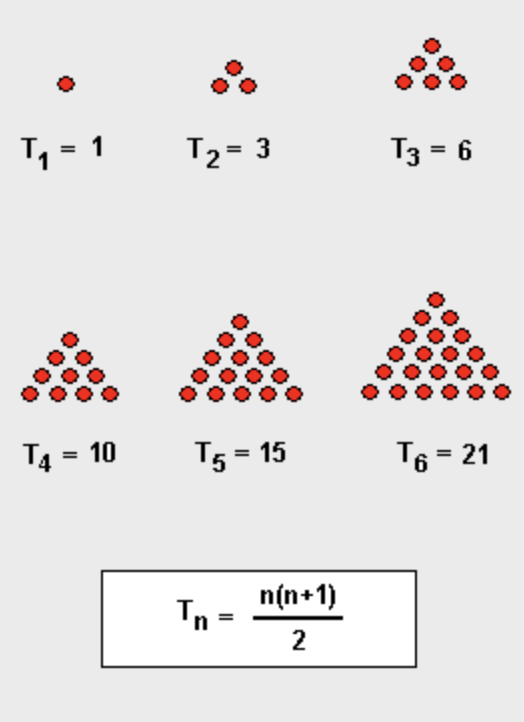
Veelhoeksgetallen zijn voorbeelden van figuratieve getallen: getallen die kunnen gevormd worden door figuurtjes te maken met bijvoorbeeld rijstkorrels of steentjes. Een veelhoeksgetal is dus een getal dat het aantal stippen is van een figuur met een in een hoekpunt geneste regelmatige veelhoek. Vanuit een hoekpunt (een buitenste stip) vertrekt dus steeds een regelmatige veelhoek.

De meest gekende zijn de driehoeksgetallen en de vierkantsgetallen of kwadraten.

Hierboven zie je hoe je het n-de driehoeksgetal kan vinden: Het is duidelijk dat

De kwadraatgetallen zijn uiteraard 1,4,9,16,… Interessant is dat sommige getallen zowel driehoeksgetallen als kwadraten zijn. Het eerste dergelijk getal is uiteraard 1. Pas bij 36 vinden we nog een getal dat in punten zowel een driehoek als een vierkant kan vormen; daarna komt 1225 en 41616.

Er bestaat een algemene formule om het n-de k-hoeksgetal te bepalen:

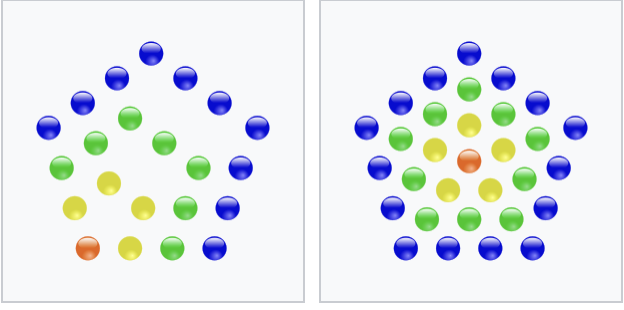
In tegenstelling tot een veelhoeksgetal gedefinieerd vanuit een hoekpunt ( zoals hierboven besproken) bestaat een gecentreerd veelhoeksgetal uit steeds groter wordende veelhoeken rond een centraal punt. hieronder zie je links een voorbeeld van een vijfhoeksgetal en rechts een voorbeeld van een gecentreerd vijfhoeksgetal

Gecentreerde veelhoeksgetallen hebben geen gemeenschappelijk hoekpunt en worden beschreven volgens volgende formule: 

Hierboven zie je het vierde vijfhoeksgetal en het vierde gecentreerd vijfhoeksgetal: en