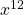Is het juist dat, indien $x^7$ en $x^{12}$ rationaal zijn, x eveneens rationaal is?

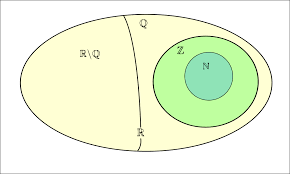
We weten dat de vermenigvuldiging en de delig door een getal, verschillend van 0, inwendige bewerkingen zijn in $\mathbb{Q}$ . Dus als $x^{12}$ en $x^7$ rationaal zijn, dan is hun quotiënt $x^5$ dat ook . Maar dan is het quotiënt van $x^7$ en $x^5$ , en dat is $x^2$ , ook een rationaal getal. Als $x^2$ rationaal is, dan ook $(x^2)^3=x^6$ . Tenslotte volgt uit het feit dat $x^6$ en $x^5$ allebei rationaal zijn dat hun quotiënt x dat ook is.Het antwoord op de gestelde vraag is dus bevestigend.

We kunnen dit ook anders oplossen: We zoeken eigenlijk twee getallen a en b zodat $(x^{12})^a:(x^7)^b=x$ , waarbij a en b gehele getallen zijn. Maar dan moet

$12a-7b=1$

Dit is een Diophantische vergelijking en omdat de grootste gemene deler van 12 en 7 gelijk is aan 1, heeft deze vergelijking oneindig veel oplossingen. De meest eenvoudige is $a=3$ en $b=5$ . Dit geeft ons in één keer ook de mogelijkheid het probleem te veralgemenen. Als we in de opgave werken met bijvoorbeeld $x^9$ en $x^{12}$ , dan klopt het niet meer: de Diophantische vergelijking $12a-9b=1$ heeft immers geen oplossingen omdat de grootste gemene deler van a en b gelijk is aan 3.