Tag archieven: diiferentiaal vergelijking

Een regendruppel…

Geplaatst op door

Een regendruppel met massa m valt onder invloed van de zwaartekracht en ondervindt een wrijving die recht evenredig mag genomen worden met de snelheid v. Bereken de snelheid in functie van t.

  • Volgens de wetten van Newton is de kracht waaraan de regendruppel onderhevig is: 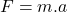F=m.a , waarbij a de versnelling is van de druppel.
  • Deze kracht F is de resultante van de zwaartekracht 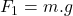F_1=m.g en de wrijving 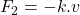F_2=-k.v, waarbij k een evenredigheidsfactor is.
  • Dus

        \[m.a=m.g-kv\]

  • Nu weten we dat a=v'. Bijgevolg is m.v'=m.g-k.v.
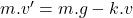  • We kunnen dit herschrijven als \frac{dv}{m.g-kv}=\frac{dt}{m}.
  • Als we beide kanten integreren krijgen we : -\frac{1}{k}\ln (m.g-k.v)=\frac{t}{m}+c, waarbij c de integratieconstante voorstelt.
  • Uitwerken geeft: m.g-k.v=A.e^{-\frac{kt}{m}.
  • Als t=0, veronderstellen we dat v=0. Hieruit vinden we dat A=m.g.
  • Vullen we dit in en lossen we op naar v, dan vinden we uiteindelijk

        \[v=\frac{m.g}{k}\Big( 1-e^{-\frac{kt}{m}\Big)\]

  • We zien dat na zekere tijd de regendruppel mat praktisch constante snelheid zal vallen.