Thomas Malhus(1766-1834) was een Brits demograaf en econoom, die vooral bekend is van zijn model voor bevolkingsgroei. Modellen voor bevolkingsgroei vormen een populair en dankbaar toepassingsgebied van differentiaalvergelijkingen en dynamische systemen.

De grootte van een populatie is intrinsiek een geheel getal en toename en afname ervan zijn discrete gebeurtenissen in de tijd. De meetgegevens die we willen moduleren zijn niet nauwkeurig tot op de eenheden, dus mogen we de verandering is de tijd eveneens modelleren alsof ze continu was.

In 1798 publiceerde Malthus het pamflet  An essay on the principle of population  waarin hij stelde dat de bevolkingsgroei de economische groei voor zou blijven. Hij veronderstelde dat de populatiegrootte op een zeker tijdstip alleen afhangt van het vorige tijdstip. Als we de bevolkingsgrootte voorstellen door P(t), dan wordt deze aanname gemodelleerd door

   

De oplossing van deze differentiaal vergelijking is

   

met exponentiële groei als en verval als .

 

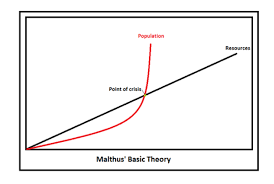
Op grond van volkstellingen kwam Malthus tot de vaststelling dat er een  exponentiële groei was voor de Engelse bevolking en dat deze bevolkingsexplosie niet kon worden bijgehouden door de lineaire groei in de voedselproductie.

 Malthus dacht dat  epidemieën en oorlog, onvoldoende waren om de exponentiële groei van de bevolking ten opzichte van de lineaire groei van de voedselproductie te corrigeren. Daarom zag Malthus als enige oplossing voor de overbevolking ‘moral restraint’; arme mensen die wisten dat ze geen gezin zouden kunnen ondersteunen, moesten volgens hem ook geen gezin stichten.