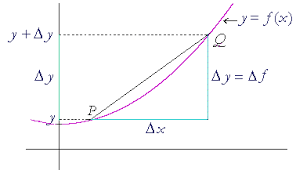
Veronderstel dat ![]() . Definieer het differentiequotiënt van
. Definieer het differentiequotiënt van ![]() , behorende bij toename
, behorende bij toename ![]() , als:
, als:
![]()
![]() is een veelterm van de
is een veelterm van de ![]() ste graad , met
ste graad , met ![]() als coëfficiënt van de hoogtse macht van
als coëfficiënt van de hoogtse macht van ![]() .
.
We kunnen op zijn beurt ook het differentiequotiënt van ![]() berekenen, bij een toename
berekenen, bij een toename ![]() . We noteren
. We noteren ![]() als
als ![]() . Ook dit is een veelterm, nu van graad
. Ook dit is een veelterm, nu van graad ![]() en met
en met ![]() als coëfficiënt van de hoogste macht van
als coëfficiënt van de hoogste macht van ![]() . Bij elke differentiequotiënt verlaagt de graad met 1. Als we
. Bij elke differentiequotiënt verlaagt de graad met 1. Als we ![]() differentiequotiënten na elkaar uitvoeren, vinden we dus een constante, en die blijkt onafhankelijk te zijn van de
differentiequotiënten na elkaar uitvoeren, vinden we dus een constante, en die blijkt onafhankelijk te zijn van de ![]() toenames
toenames ![]() . We krijgen :
. We krijgen :
![]()
Kies ![]() en schrijf
en schrijf ![]() in plaats van
in plaats van ![]() , dan volgt:
, dan volgt:
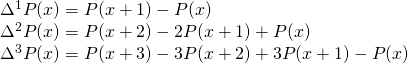
We besluiten hieruit:
![Rendered by QuickLaTeX.com \[a_n.n!=\Delta^nP(x)= \sum_{k=0}^n(-1)^k\binom{n}{k}P(x+n-k)\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-ab065617069a871c609379661431790a_l3.png?media=1678572382)
We kunnen bovenstaande formule nog vereenvoudigen door ![]() in plaats van
in plaats van ![]() als variabele te nemen. Dit mag omdat de substitutie
als variabele te nemen. Dit mag omdat de substitutie ![]() in
in ![]() een veelterm geeft met dezelfde kopcoëfficiënt.
een veelterm geeft met dezelfde kopcoëfficiënt.
![Rendered by QuickLaTeX.com \[a_n.n!= \sum_{k=0}^n(-1)^k\binom{n}{k}P(x-k)\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-ffeba57122f70dedd2bfaf9c3672370c_l3.png?media=1678572382)
Als we ![]() vervangen door
vervangen door ![]() , dan wordt, volgens dezelfde opmerking als hierboven, deze formule:
, dan wordt, volgens dezelfde opmerking als hierboven, deze formule:
![Rendered by QuickLaTeX.com \[a_n.n!= \sum_{k=0}^n(-1)^{n-k}\binom{n}{k}P(x+k)\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-edafc41b31f67049cf60c965dba87cc5_l3.png?media=1678572382)
Opmerkingen:
- Neem
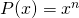 , dan wordt bovenstaande formule:
, dan wordt bovenstaande formule: 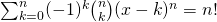
- We controleren voor
 . Het linkerlid wordt
. Het linkerlid wordt 
- Omdat in vorig punt het rechterlid een constante is, kan je in het linkerlid
 vervangen door om het even welke uitdrukking, bijvoorbeeld :
vervangen door om het even welke uitdrukking, bijvoorbeeld :