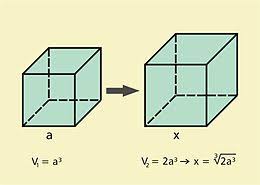
Het probleem van het ’verdubbelen van de kubus’ luidt: construeer de ribbe van een kubus die een twee keer zo grote inhoud heeft als die van een gegeven kubus.
Volgens de legende consulteerden de burgers van Athene het orakel van Apollo in Delos in 430 v.Chr. om te horen hoe zij de pest, die een vernietigende werking had op hun land, moesten bestrijden. Het orakel antwoordde dat, om de pest te stoppen, zij hun altaar in grootte moesten verdubbelen. De Atheners verdubbelden plichtsgestrouw elke zijde van het altaar, en de pest verslechterde! De correcte interpretatie was dat zij het volume van het altaar moesten verdubbelen, niet slechts de lengte van de zijdes; dit bleek een zeer moeilijk oplosbaar probleem. Ten gevolge van deze legende wordt het probleem vaak het Delische probleem genoemd.
De oude Grieken poogden de constructie uit te voeren met behulp van ’hun’ constructiemiddelen: de passer en liniaal. Maar het bleek daarmee niet te kunnen.
Vele eeuwen later werd bewezen dat de oplossing met passer en liniaal niet mogelijk is.
Echter, er zijn wel andere middelen om de constructie uit te voeren. Zo heeft Nicomedes (ca. 180 v.Chr.) de conchoïde, een bijzondere kromme lijn, ontdekt waarmee hij de oplossing kon construeren.
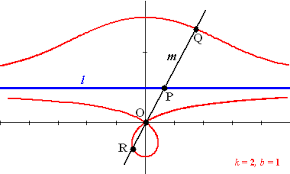
Wij geven een eenvoudige oplossing die toegeschrevn wordt aan Plato. Stel dat de gegeven kubus een ribbe heeft met lengte a en de gevraagde kubus een ribbe met de lengte x. Dan kunnen we het probleem als volgt omschrijven:
Gegeven: a; Construeer: een x die voldoet aan
![\[x^3 = 2a^3\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-aebb7592b0336e2b49fc60ddf350f60b_l3.png?media=1678572382 "Rendered by QuickLaTeX.com")
;
Denk je een rechthoekig trapezium ABCD waarin de diagonalen loodrecht op
elkaar staan .
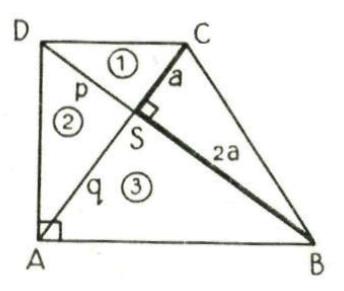
Als we SC de lengte a geven en SB de lengte 2a, dan zal DS of p dus, gelijk zijn aan de gevraagde afstand. Het is duidelijk dat de driehoeken 1,2 en 3 allen gelijkvormig zijn ( gelijk hoeken via verwisselende binnenhoeken of complementen van verwisselende binnenhoeken). Hieruit volgt dat 
of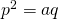 
. Verder is ook 
of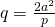 
. Als we deze twee formules samnevoegen krijgen we 
en dus is p het gewenste antwoord.
In deze tekst onderzoeken welke we getallen er construeerbaar zijn met de klassieke constructieapparaten, passer en liniaal. Verder bestuderen we ook de structuur van de verzameling van alle construeerbare getallen. We komen zo tot een modern algebraïsch bewijs van de onmogelijkheid om met passer en liniaal een kubus te verdubbelen. Dit is een welbekend probleem uit de oude Griekse meetkunde. Zo zien we dat algebra en meetkunde enerzijds en oude en moderne wiskunde anderzijds erg nauw samenlopen.