Tag archieven: delers van een getal

Product van de delers van een getal

Geplaatst op door

Noteer met i het aantal delers van een gegeven natuurlijk getal n, dat verschilt van 0. Kan je dan een formule vinden voor het product van al de delers van n?

Stel del(n) = \{d_1,d_2,\cdots,d_i\}  en noteer met P(n) het product van alle delers . Dan is P(n) = d_1*d_2*\cdots*d_i=d_i*\cdots*d_2*d_1. Vermenigvuldigen we deze twee uitdrukkingen met elkaar : P(n)^2=n^i , dan vinden we

    \[P(n)=\sqrt{n^i}\]

Enkele voorbeelden:

  • del(7) = (1,7} , dus P(7)=\sqrt{7^2}=7 en 1*7=7
  • del(9) = (1,3,9} , dus 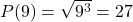P(9)=\sqrt{9^3}=27 en 1*3*9=27.
  • del(12) = (1,2,3,4,6,12} , dus 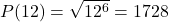P(12)=\sqrt{12^6}=1728 en 1*2*3*4*6*12=1728.