Voor welke waarde van  is
is  deelbaar door
deelbaar door 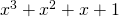 ?
?
Antwoord
- Een veelterm A is deelbaar door een veelterm B als alle nulwaarden van B ook nulwaarden zijn van A.
- Nu is
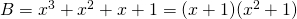 , dus de nulwaarden van B zijn :
, dus de nulwaarden van B zijn :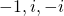 .
. - Omdat
 enkel gehele coëfficiënten heeft kunnen we de stelling van d’Alembert gebruiken die zegt dat als
enkel gehele coëfficiënten heeft kunnen we de stelling van d’Alembert gebruiken die zegt dat als 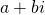 een nulwaarde is, dan is
een nulwaarde is, dan is 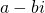 dat ook.
dat ook. - We moeten dus enkel eisen dat
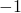 en
en  nulwaarden zijn van A.
nulwaarden zijn van A. - Dan moet
 of
of 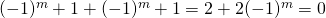 . Hieruit volgt dat
. Hieruit volgt dat 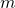 oneven moet zijn.
oneven moet zijn. - Verder moet ook
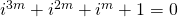 . Dus moet
. Dus moet  . Als
. Als 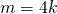 dan is
dan is 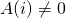 . In alle andere gevallen is
. In alle andere gevallen is  wel gelijk aan
wel gelijk aan  .
. - De twee voorwaarden samen geven dat m gewoon oneven moet zijn.
- Dus is
 deelbaar door
deelbaar door  als
als 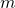 oneven is.
oneven is.
