Tag archieven: deelbaar door 7

Deelbaarheid door 3, 7, 9 en 11

Geplaatst op door

Iedereen weet dat een getal deelbaar is door 2 als het laatste cijfer, in zijn decimale notatie, even is.  Want een getal n kan je schrijven als n=10k+u, waarbij u het laatste cijfer is in de decimale notatie van n. Het is duidelijk dat 2|n als en slechts als 2|u. Hetzelfde geldt voor 5.

Elk getal n  is te schrijven  als n=100k+u, waarbij u het getal is gevormd door de laatste 2 cijfers van n. Bijgevolg is n deelbaar door 4 of 25 als de laatste 2 cijferss deelbaar zijn door 4 of 25.

Hoe kunnen we nu zien of een getal deelbaar is door 3, 9 of 11? Bekijken we eerst een stelling over congruenties met veeltermen met gehele cëfficiënten:

Stel f(x)=\sum_{k=0}^nc_kx^k met c_i \in \mathbb{Z}. Als a \equiv b mod m, dan is f(a) \equiv f(b) mod m.

Neem nu a=\sum_{k=0}^na_k10^k, de decimale schrijfwijze van het getal a en noteer s=\sum_{k=0}^na_k en t=\sum_{k=0}^n(-1)^ka_k. Het is duidelijk dat a=f(10) met f(x)=\sum_{k=0}^na_kx^k en dat s=f(1). Omdat 10 \equiv 1 mod 9, geldt volgens vorige stelling dat f(10) \equiv f(1) mod 9 of met andere woorden : een getal is deelbaar door 9 als de som van haar cijfers deelbaar is door 9. Analoog voor deelbaarheid door 3. Het bewijs voor deelbaarheid door 11 volgt uit het feit dat 10 \equiv -1 mod 11 en t=f(-1).

Besluit:
Een getal is deelbaar door 3 of 9 als de som van de cijfers van het getal deelbaar is door 3 of 9.
Een getal is deelbaar door 11 als 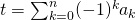t=\sum_{k=0}^n(-1)^ka_k deelbaar is door 11.

 

Een toemaatje : deelbaarheid door 7: Omdat 10^3 \equiv -1 mod 7 kan je  deelbaarheid door 7 als volgt vinden: Verdeel het getal van rechts naar links in groepjes van 3. Voor zie elk groepje alternerend met een + en – teken. Een getal is deelbaar door 7 las de som van die getallen deelbaar is door 7. Zo is bijvoorbeeld  2 345 678 902 deelbaar door 7 omdat 902 -678 + 345 – 2 = 567 en dat is deelbaar door 7 .