Dit probleem werd 400 jaar geleden aangekaart door de Franse wiskundige Claude Gaspard Bachet de Méziriac(1581-1638): wat is de kleinst mogelijke verzameling gewichten waarmee je iedere gehele kilo van 1 tot 40 kan afwegen?

Eigenlijk staat dit raadsel in het liber Abaci van Leonardo Pisano(1202). Bachet was een dichter, vertaler en tolk en was de schrijven van het raadselboek Problèmes plaisants et délectable qui se font par les mombers(1612). In dit standaardwerk voor creatieve wiskunde staat onder andere dit probleem.

Elk natuurlijk getal tussen 1 en 40 kan je in het drietallig talstelsel schrijven. Daarvoor heb je enkel de getallen 1,3,9 en 27 nodig. Dit zijn onze basisgewichten. Maar hoe kunnen we dan alle gewichten tussen 1 en 40 afwegen?

• In de drietallige schrijfwijze komen alleen nullen en enen voor: neem bvb. 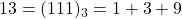. Dus kan je met de gewichten 1,3,9 een gewicht van 13 afwegen.
• Wat te doen als er een 2 voorkomt in de drietallige schrijfwijze? Neem bvb. 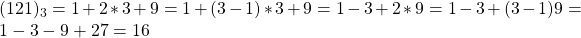 Je kan dit dan schrijven als 1+27 = 16 +3 +9. Leg dan de gewichten 1 en 27 op de linker schaal en de gewichten 3,9 samen met het gewicht 16 op de rechterschaal.
• Omdat de som van 1,3,9 en 27 juist 40 is kan je dus zo elk gewicht tussen 1 en 40 afwegen!