Wiskunde is leuk

Opgave 12

Geplaatst op 2 maart 2018 door admin

Construeer de ingeschreven cirkel van een driehoek waarbij twee hoekpunten ontoegankelijk zijn.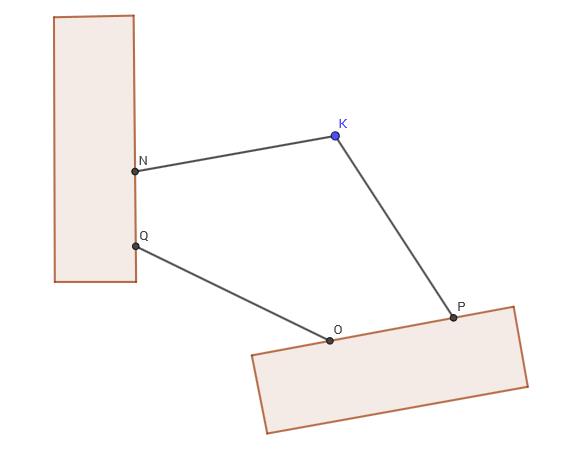

Antwoord

We kiezen een rechte ( rood) die twee zijden snijdt en bepaal de spiegelbeelden van die zijden ( blauwe stippellijn).
Bepaal het snijpunt van die stippellijnen: T en bepaal de deellijn
( blauw )van de hoek in T.
Spiegel die lijn terug rond de rode rechte ( groene lijn) en bepaal het snijpunt U met de deellijn (paarse lijn )van de driehoek die je wel kon tekenen (vanuit K).
U is het middelpunt van de ingeschreven cirkel.

Constructies in verband met ontoegankelijkheid

Geplaatst op 14 februari 2018 door admin

We bestuderen constructies die we normaal gesproken wel kunnen uitvoeren, maar die nu niet uit te voeren zijn omdat bepaalde delen van de figuur ontoegankelijk zijn. Om zulke constructies uit te voeren zijn spiegelingen rond een as uitermate geschikt. We weten immers dat een spiegeling evenwijdigheid, loodrechtheid en ook afstanden en hoeken bewaart. Hierdoor wordt het mogelijk bepaalde gegevens toch bereikbaar te maken.

Bepaal de bissectrice van de twee gegeven rechten.}

Teken een willekeurige rechte $m$ die de twee gegeven rechten (die we $a$ en $b$ noemen) snijdt.
Spiegel de gegeven rechten rond $m$ : $a'$ en $b'$ .
Bepaal het snijpunt $S$ van $a'$ en $b'$ .
Construeer de bissectrice $d$ van $a'$ en $b'$ . Dit is een basisconstructie.
Bepaal tenslotte het spiegelbeeld $d'$ , bij spiegeling van $d$ rond $m$ .