Tag archieven: constructies

Constructies in verband met verdeling

Geplaatst op door

Het gaat hier over constructies waarbij een bepaald element in een bepaalde verhoudinhg moet verdeeld worden.

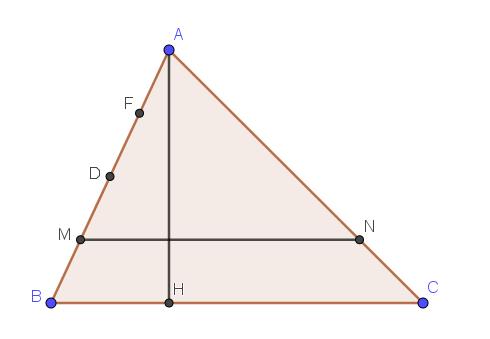
Voorbeeld: Verdeel een gegeven driehoek ABC , door een evenwijdige MN aan BC , zodat de oppervlakte van driehoek AMN gelijk is aan \dfrac{9}{16} van de oppervlakte van driehoek ABC.

 

Noteer de oppervlakte van driehoek ABC door S(ABC). Dan moet
S(AMN) = \dfrac{9}{16} S(ABC) = \dfrac{9}{16}.\dfrac{1}{2}a.h. En dit betekent dat men een verdeling moet vinden zodanig dat \dfrac{9}{16}a.h=\dfrac{a}{x}.\dfrac{h}{x}. Hieruit volgt dat x=\dfrac{4}{3}, zodat de te construeren a’ en h’ gelijk moeten zijn aan a'=\dfrac{3}{4}a en h'=\dfrac{3}{4}h.

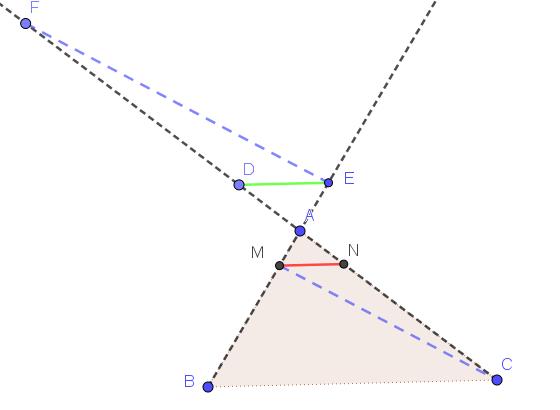
Verdeel AB in 4 gelijke delen en trek door M een evenwijdige met BC. Via de stelling van Thales weten we dat |MN|=\dfrac{3}4}|BC| en ook de hoogtes van de twee driehoeken AMN en ABC verhouden zich volgens de breuk \dfrac{3}{4}

 

Constructies in verband met verhoudingen

Geplaatst op door

In tegenstelling tot de constructies in verband met ontoegankelijkheid, waarbij spiegelingen gebruikt worden, zijn het nu de homothetieën die een hoofdrol spelen. Hierbij worden de afstanden niet bewaard, maar wel de onderlinge verhoudingen. Hierdoor wordt het mogelijk bepaalde gegevens in een zelfgekozen situatie te simuleren  om ze dan door een homothetie over te brengen naar de gekozen situatie. Hiervoor maken we gebruik van de stelling van Thales

De belangrijke keuze die men dient te maken is het kiezen van het centrum en een koppel punten.

Voorbeeld: Construeer in een driehoek ABC een lijnstuk [MN] met M op AB , N op AC en MN evenwijdig met BC zodat |NC|=3|MN|

  • Verleng AB en AC en teken DE evenwijdig met BC.
  • Construeer F op AC zodat |FD|=3|DE|.
  • Neem de homothetie met centrum A en met koppel (C,F).
  • Bepaal het beeld van DE onder deze homothetie: Dit geeft het gevraagde lijnstuk MN.