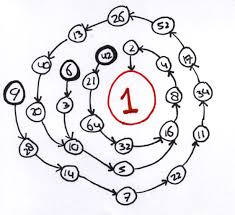
Neem een natuurlijk getal n. Als het even is, deel het door 2. Als het oneven is, vermenigvuldig je het met 3 en tel er 1 bij op. Met de uitkomst doe je hetzelfde, en dat blijf je maar herhalen.
Neem bijvoorbeeld 6, dan ontstaat volgende rij : 6,3,10,5,16,8,4,2,1. We noemen dit de Collatz rij van 6. De lengte van deze Collatz rij is 9. De lengte van dergelijke rij kan snel oplopen. Zo is de lengte van de Collatz rij van 27 gelijk aan 111.
Het 3n + 1-vermoeden zegt dat bovengenoemd iteratieproces bij iedere mogelijke startwaarde altijd een keer bij 1 zal uitkomen. De precieze oorsprong van het 3n + 1- vermoeden is niet helemaal duidelijk. In de jaren dertig was Lothar Collatz( 1910-1990), een Duitse wiskundige, met soortgelijke problemen bezig, en het 3n + 1-probleem wordt algemeen aan hem toegeschreven. Het is tot op heden nog steeds niet bewezen.
Er zijn enkele aanwijzingen dat het vermoeden van Collatz juist is. Voor alle getallen onder 
is inmiddels gecontroleerd dat ze aan het vermoeden voldoen. Het probleem met het controleren is dat het alleen het vermoeden kan weerleggen. Als het vermoeden waar is, kan er geen bewijs voor gevonden worden op deze manier.
