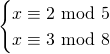Controleer voor elk natuurlijk getal vanaf 7 of 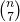 deelbaar is door 12 en bereken de fractie van dergelijke getallen. Zoek de limiet van die fractie als je steeds meer getallen controleert.
deelbaar is door 12 en bereken de fractie van dergelijke getallen. Zoek de limiet van die fractie als je steeds meer getallen controleert.
Antwoord

![Rendered by QuickLaTeX.com \[\begin{cases} n \equiv 0,1,2,3,4,5,6 \text{ mod } 9 \\ n \equiv 0,1,2,3,4,5,6 ,8,9,10,12,13,14 \text{ mod } 16\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-bdd2e4010102ab0476ddcbbad926ea37_l3.png?media=1678572382)


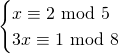 of
of