
De Chebyshev-veeltermen ![]() zijn genoemd naar Pafnoeti Lvovitsj Chebyshev en zijn gedefinieerd door
zijn genoemd naar Pafnoeti Lvovitsj Chebyshev en zijn gedefinieerd door ![]() uit te drukken in functie van
uit te drukken in functie van ![]() :
:
![]()
Zo is ![]() en
en ![]() . Omdat
. Omdat ![]() is
is ![]() . We weten ook dat
. We weten ook dat ![]() , dus is
, dus is ![]() .
.
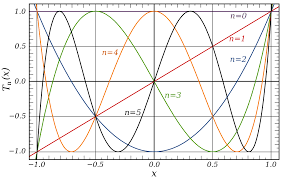
Dat ![]() een veelterm is van graad n volgt uit de formule van Lemoivre. Andere Chebyshev veeltermen:
een veelterm is van graad n volgt uit de formule van Lemoivre. Andere Chebyshev veeltermen:
![]()
![]() .
.
Het onderstaande driehoekig schema geeft een middel aan om de coëfficiënten te bepalen. Elk getal uit de driehoek bekom je door vanaf die positie alle getallen op de diagonaal naar rechtsboven bij elkaar op te tellenen hiervan dan alle getallen op de diagonaal naar linksboven af te trekken. Zo is bijvoorbeeld 18 = 5 + 1 + 0 – (-20) – 8.
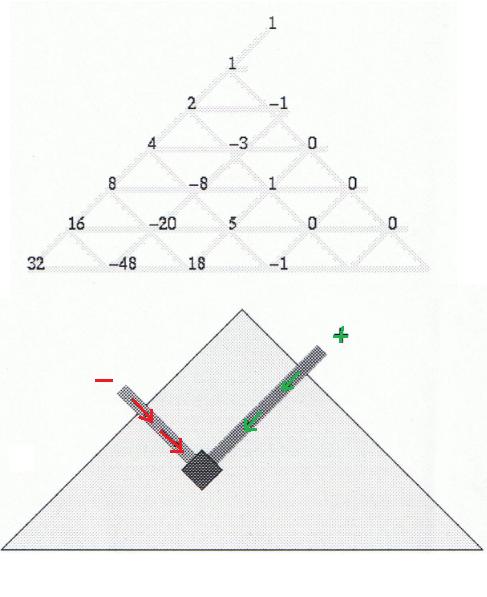
Je kan deze veeltermen ook krijgen via een recursie formule:
![]()
Bovendien zijn de Chebyshev veeltermen ook oplossingen van volgende differentiaalvergelijking:
![]()
