Pareltjes uit de oude doos!
De stelling van Ceva zegt : AD, BE en CF snijden elkaar is 1 punt is equivalent met
![\[\dfrac{|AF|}{|FB|}.\dfrac{|BD|}{|DC|}.\dfrac{|CE|}{|EA|}=1\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-2b3ce5215a4adff9101432676ed24db8_l3.png?media=1678572382 "Rendered by QuickLaTeX.com")
Hierbij moeten de verhoudingen opgevat worden als verhoudingen van de overeenkomstige vectoren, zodat de verhouding negatief is als de vectoren tegengesteld zijn. De transversalen AD, BE en CF worden ook wel Cevianen genoemd. De stelling werd voor het eerst bewezen door Giovanni Ceva in zijn werk De lineis rectis uit 1678. 
Als we stelling van Ceva ‘vertalen’ ( punt wordt lijn en lijn wordt punt, lijn gaat door punt wordt punt ligt op lijn, snijpunt van 2 lijnen wordt verbindingslijnstuk van 2 punten) krijgen we de stelling van Menelaos:
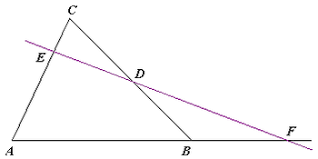
Drie punten, D,E en F, gelegen op de zijden van een driehoek, liggen op één lijn als en slechts als
![\[\dfrac{|AF|}{|FB|}.\dfrac{|BD|}{|DC|}.\dfrac{|CE|}{|EA|}=-1\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-641298ca797dba8024416cfefed0458e_l3.png?media=1678572382 "Rendered by QuickLaTeX.com")
Merk op dat de verhouding positief is als F tussen A en B ligt, en negatief als F buiten het lijnstuk AB ligt.