Er bestaat een manier om de structuur van een groep visueel voor te stellen. Het was de Engelse wiskundige Arthur Cayley die in 1878 als eerste gebruik maakte van de theorie van de grafen om dit te doen. We spreken dan ook van een Cayley – graaf van een groep.
Gegeven zijn een groep G en een verzameling van generatoren van de groep. De Cayley – graaf van G is dan een gekleurde en gerichte graaf die opgebouwd is volgens de volgende regels:
- Met elk element van de groep correspondeert 1 knoop van de graaf.
- Voor elke generator gebruiken we een aparte kleur.
- Als a een generator is, dan gaat er, in de kleur die bij a hoort, een gerichte zijde van elk element g van de groep naar het element g.a.
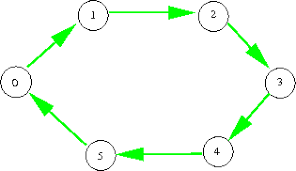
Voor de cyclische groep van orde 6 ( ![]() ) is de graaf zeer eenvoudig: De generator is 1.
) is de graaf zeer eenvoudig: De generator is 1.
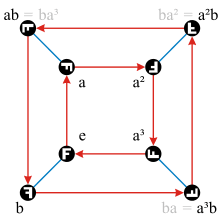
Voor de dihaedergroep ![]() is het al wat moeilijker: de generatoren zijn a en b. De rode pijl geeft de rechtervermenigvuldiging met a en de blauwe de rechtervermenigvuldiging met b. Bij de blauwe pijl ontbreekt de pijlrichting omdat de pijl heen en terug gaat.
is het al wat moeilijker: de generatoren zijn a en b. De rode pijl geeft de rechtervermenigvuldiging met a en de blauwe de rechtervermenigvuldiging met b. Bij de blauwe pijl ontbreekt de pijlrichting omdat de pijl heen en terug gaat.