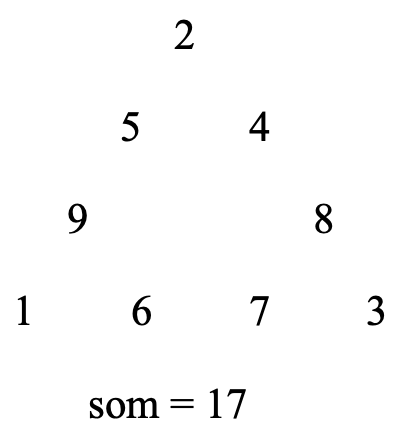
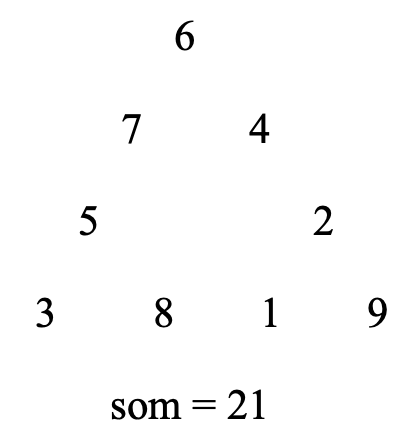
Plaats de cijfers van 1 tot en met 9 in de cirkeltjes in het diagram zodat de som van de vier cijfers langs de drie zijden gelijk is aan 17. En hoe kan je ze rangschikken zodat de som langs de drie zijden telkens gelijk is aan 20? Is er een andere som mogelijk?
Deze puzzel komt uit het boek The Moscow puzzels van Boris Kordemsky(1907-1999), een wiskundedocent uit Moskou.
Spoiler
- Noteer de som langs de drie zijden door x en de som van de elementen in de hoekpunten door s.
- de som van alle cijfers 1 tot 9 is 45.
- Dus 45=3x – s. Hieruit volgt dat s een drievoud moet zijn.
- Voor x = 17 vinden we s = 6 en krijgen we volgende oplossing:
- voor x = 20 vinden we s= 15 en vinden we de oplossingen:
- We vinden ook een oplossing voor x = 21 met s = 18:
- Andere oplossingen hebben we niet gevonden.