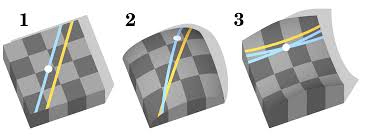
De meetkunde, die we dagelijks gebruiken, wordt Euclidische meetkunde genoemd, ter ere van Euclides, die tussen 330 en 320 voor Christus een aantal boeken, genaamd „Elementen” geschreven heeft.
Hierin wordt de meetkunde opgebouwd met stellingen vertrekkend van een vijftal postulaten of axioma’s:
1. Door 2 verschillende punten gaat juist 1 rechte.
2. Een lijnstuk kan naar beide kanten onbeperkt worden
verlengd.
3. Er kan met elk middelpunt en elke straal een cirkel
getrokken worden.
4. Alle rechte hoeken zijn gelijk.
5. Door een punt P buiten een rechte , gaat precies één rechte
die evenwijdig loopt met de eerste rechte.
Dit laatste axioma staat bekend als het parallellenpostulaat.
Eeuwen heeft men gedacht dat men dit postulaat kon bewijzen aan de hand van de andere vier axioma’s. Trouwens de formulering van het parallellenpostulaat was oorspronkelijk anders. De gegeven formulering komt van John Playfair. Deze formulering stamt uit 1795 en staat bekend als “Playfair’s axioma” . Een andere gelijkwaardige formulering van dit postulaat is dat de hoekensom van een driehoek gelijk is aan 180°.
Het duurde tot de 19 de eeuw voor het juist inzicht er kwam en wel bij 3 wiskundigen ongeveer gelijktijdig en waarschijnlijk onafhankelijk van elkaar: C.F.Gauss, J.Bolyai en I.Lobatschefsky.
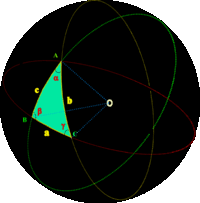
Het was Joha,, Bolyai die tot het inzicht kwam dat het mogelijk was een meetkunde op te stellen, waarin door een punt buiten een rechte oneindig veel rechten gaan die de gegeven rechte niet snijden. Hij publiceerde zijn ideeën in 1832 en gaf zo gestalte aan de hyperbolische meetkunde. De som van de hoeken van een driehoek is hier minder dan 180°. In de hyperbolische meetkunde wordt dus niet meer aan het parallellenpostulaat voldaan.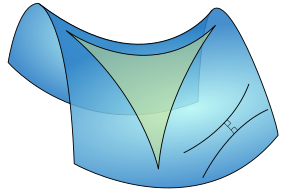 
Later werd ook de elliptische meetkunde ontdekt. Elliptische meetkunde is een niet-Euclidische meetkunde, waarbij door een punt buiten een rechte geen andere rechten bestaat die de gegeven rechte niet snijdt.
De gewone meetkunde is dus niet de meetkunde, maar een meetkunde. Met andere axioma’s krijgen we een ander soort meetkunde.
