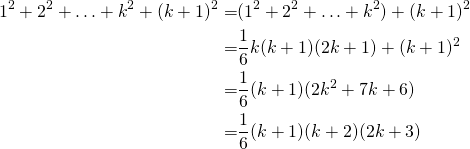Een rij van getallen kan je geven met behulp van een recursief voorschrift zoals bijvoorbeeld : ![]() en
en ![]() . Soms kan je uit dit recursief voorschrift een expliciete formule afleiden voor de algemene term van de rij. Soms kan dat niet, maar is het mogelijk, via recursie, de parameters te herleiden tot waarden waarvoor je het probleem wel kan oplossen.
. Soms kan je uit dit recursief voorschrift een expliciete formule afleiden voor de algemene term van de rij. Soms kan dat niet, maar is het mogelijk, via recursie, de parameters te herleiden tot waarden waarvoor je het probleem wel kan oplossen.
Een eerlijk muntstuk wordt 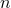 keer opgeworpen. Wat is de kans op twee opeenvolgende keren kop ergens in de rij worpen?
keer opgeworpen. Wat is de kans op twee opeenvolgende keren kop ergens in de rij worpen?
- Noteer met
 de kans dat er nergens twee keer kop na elkaar voorkomt is de rij van n worpen.
de kans dat er nergens twee keer kop na elkaar voorkomt is de rij van n worpen. - Het is duidelijk dat
 en
en 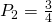 .
. - Stel
 . Dan zijn er twee mogelijkheden naargelang de eerste worp kop of munt is.
. Dan zijn er twee mogelijkheden naargelang de eerste worp kop of munt is. - Als je eerst munt gooit, dan is de kans dat je nergens twee keer kop na elkaar hebt in de volgende
 worpen gelijk aan
worpen gelijk aan 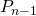 .
. - Gooi je eerst kop, dan moet de tweede worp munt zijn, want anders zou je twee keer kop na elkaar hebben. De kans dat je nergens twee keer kop na elkaar hebt in de volgende
 worpen gelijk aan
worpen gelijk aan 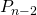 .
. - Uit de vorige twee punten vinden we tenslotte dat
![Rendered by QuickLaTeX.com \[P_n=\frac{1}{2}P_{n-1}+\frac{1}{4}P_{n-2}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-119de26fcd44ab4623f5fc327ef8ceb0_l3.png?media=1678572382)
- Dit kan je herleiden tot
 . Of via
. Of via  :
:
![Rendered by QuickLaTeX.com \[S_n=S_{n-1}+S_{n-2}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-01e5606300397d8b66fcf6f317f91e91_l3.png?media=1678572382)
- Dit is de rij van Fibonacci, waarbij
 het n+2 de getal in de rij van Fibonacci is. Dus
het n+2 de getal in de rij van Fibonacci is. Dus  . De gezochte kans op twee opeenvolgende keren kop ergens in de rij van
. De gezochte kans op twee opeenvolgende keren kop ergens in de rij van 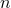 worpen, met
worpen, met  is dan
is dan  .
.