9801

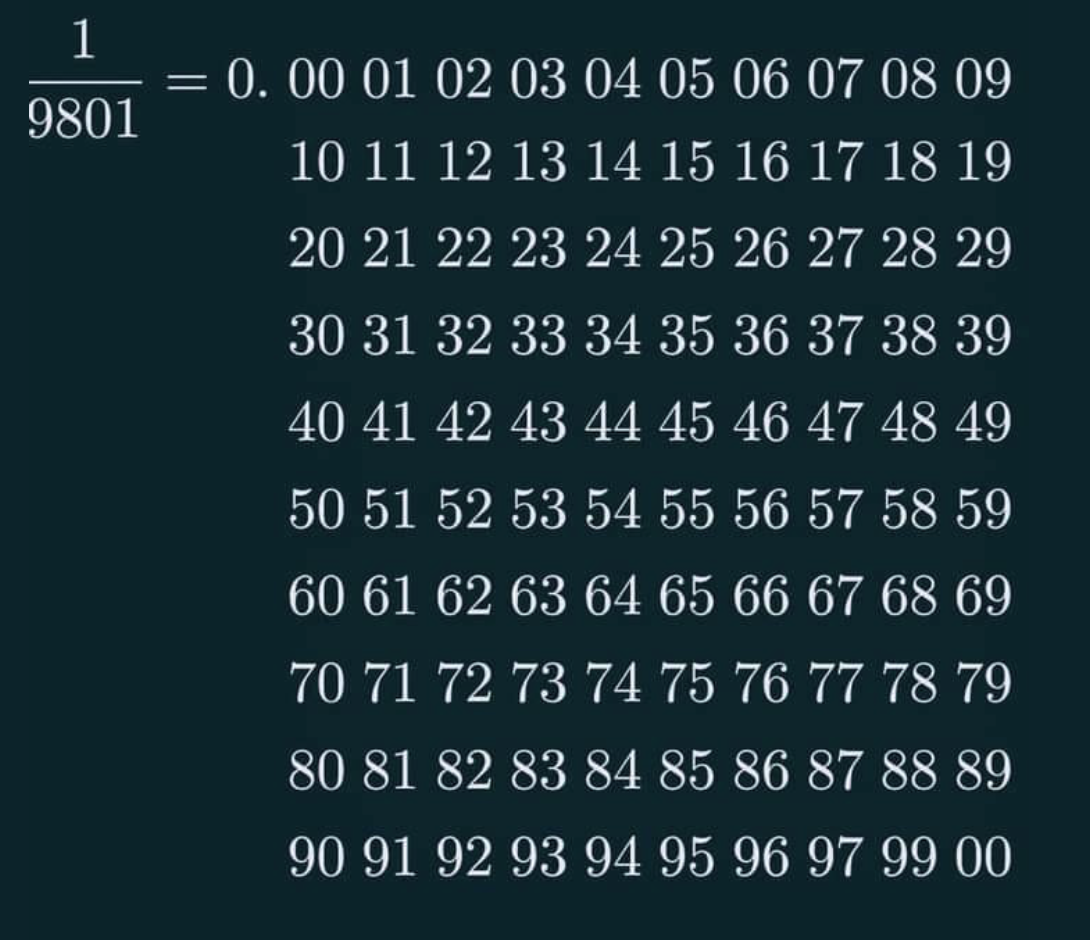
Mooie decimale schrijfwijze! Kan je dit verklaren? Nu is . Verder is . Je kan gemakkelijk narekenen dat     Vervangen we nu hierin x door , dan krijgen we de gewenste decimale schrijfwijze. Maar waarom ontbreekt hierin de 98? In de uitwerking staan de som .  Wat gebeurt er met en ?