De grote wis- en natuurkundige Leonhard Euler (1707-1783) publiceerde
in 1736 het zogenaamde Koningsberger bruggenprobleem. De stad Koningsbergen, die sinds 1945 Kaliningrad heet, ligt aan de oevers van en op twee eilanden in de rivier de Pregel. De oevers en de eilanden waren in Eulers tijd verbonden door zeven bruggen. De Koningsbergers waren gewend ’s zondags een lange wandeling door de stad te maken en Euler vroeg zich nu af of hij een wandeling zou kunnen ontwerpen, waarbij elk der bruggen juist eenmaal zou gepasserd worden.
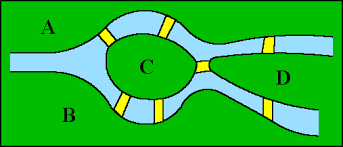
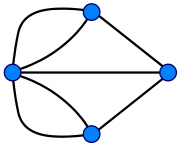
We vereenvoudigen de plattegrond van Koningsbergen door elk der vier stadsdelen A, B, C en D door een punt voor te stellen en elk der zeven bruggen door een lijn. Een dergelijke figuur noemt men een graaf. De graaf in ons probleem heeft vier hoekpunten en zeven kanten. We kunnen het bruggenprobleem nu zo formuleren: Is het mogelijk de graaf zo te doorlopen, dat daarbij elk der kanten slechts éénmaal gepasseerd wordt? Beginnen we bijv. bij het hoekpunt A, dan moet daar een ,,uitgaande kant”, maar ook een ,,inkomende kant” zijn. Telkens als we via een der kanten in een hoekpunt aankomen, moet daar weer behalve de ,,inkomende” ook een ,,uitgaande kant” zijn. Hieruit blijkt, dat als we de graaf zo willen doorlopen, dat we elk der kanten slechts eenmaal gebruiken, er bij elk hoekpunt een even aantal kanten moeten samenkomen. Aangezien dat niet het geval is, is het onmogelijk een wandeling door Koningsbergen te organiseren, waarbij elk der bruggen slechts éénmaal doorlopen wordt.