Op hoeveel manieren N kan je 28 schrijven als som van verschillende natuurlijke getallen ( ![]() )?
)?
- Noteer
 als het aantal mogelijkheden om n te schrijven als som van k verschillende natuurlijke getallen, verschillend van 0.
als het aantal mogelijkheden om n te schrijven als som van k verschillende natuurlijke getallen, verschillend van 0. - Het is niet zo moeilijk om
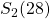 uit te rekenen: 1+27,2+26,…13+15. Dus
uit te rekenen: 1+27,2+26,…13+15. Dus  .
. - Omdat
 is
is 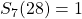 . Bovendien zal voor
. Bovendien zal voor 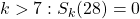 .
. - Berekenen we eerst
 . Stel dus dat
. Stel dus dat  en neem
en neem 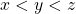 . Als
. Als  , dan is
, dan is  een drietal met som 25, dus een mogelijkheid uit
een drietal met som 25, dus een mogelijkheid uit  . Omgekeerd kan je ook met elke mogelijkheid van
. Omgekeerd kan je ook met elke mogelijkheid van  , een mogelijkheid van
, een mogelijkheid van  laten corresponderen met elementen groter dan 1.
laten corresponderen met elementen groter dan 1. - Stel echter dat x=1, dan is
 een tweetal met som 25 en dus een mogelijkheid uit
een tweetal met som 25 en dus een mogelijkheid uit 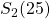 .
. - Uit vorige redeneringen volgt
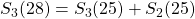 of algemener:
of algemener: ![Rendered by QuickLaTeX.com \[S_3(n)=S_3(n-3)+S_2(n-3)\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-2eee861396db2e46bf6e70df05fae7d3_l3.png?media=1678572382)
- Herhaaldelijk toepassen van die formule geeft:
 .
. - Maar
 als n even is en
als n even is en 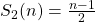 als n oneven is. Hieruit volgt dat
als n oneven is. Hieruit volgt dat 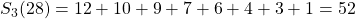 .
. - Om
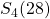 te berekenen gebruiken we een analoge formule
te berekenen gebruiken we een analoge formule 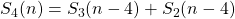 . Idem voor
. Idem voor 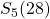 en
en 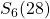 .
. - Enkele berekingen staan in volgende tabel en zo vinden we
![Rendered by QuickLaTeX.com \[N=13+52+84+57+14+1=221\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-93cca0a902b7d049b34bab863bfb8d38_l3.png?media=1678572382)


