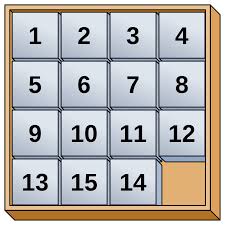
De schuifpuzzel is een puzzel, meestal op een bord van 4  op 4 met 15 verschillende stukken en 1 leeg veld; Het wordt dan ook   15-puzzel genoemd, maar bestaat ook in andere afmetingen. De bedoeling is om de stukken terug in de goede volgorde te krijgen door de stukken te schuiven.

De oorspronkelijke versie van dit spel werd in 1874 ontwikkeld door de New Yorkse postdirecteur Noyes Palmer Chapman. De vierkantjes zaten los en de speler kon ze in willekeurige volgorde neerleggen en dan proberen de puzzel door schuiven op te lossen. In de afbeelding hierboven uit Sam Loyds Cyclopedia waren in de beginpositie de getallen 14 en 15 van plaats gewisseld. 

Niet elke beginpositie is oplosbaar. Wiskundigen hebben onderzocht welke beginopstellingen kunnen worden opgelost. Neem bijvoorbeeld bovenstaande puzzel, beter afgebeeld als:

Is dit oplosbaar?

Twee speltoestanden worden als equivalent gedefinieerd als de ene door een aantal malen schuiven in de andere kan worden overgevoerd. Deze relatie is een equivalentierelatie.  Of  de puzzel oplosbaar is betekent dus of bovenstaande schikking equivalent is met de begintoestand. Men kan aantonen dat twee speltoestanden equivalent zijn als de pariteit van de permutatie van de 16 elementen die de ene in de andere overvoert gelijk aan die van de ‘afstand’  tussen de lege velden van de twee speltoestanden (dit betekent dat de twee lege velden zoals bij een schaakbord dezelfde of een verschillende kleur hebben). Wat geeft dit nu voor onze opgave?

• de lege vakken staan in begin en eind situatie opdezelfde plaats: dus pariteit 0
• De eindsituatie wordt bekomen uit de beginsituatie via 1 transpositie ( 1 omkering: 14 versus 15); Dus is de permutatie oneven en heeft pariteit 1.
• De twee pariteiten zijn verschillend en dus is de puzzel onoplosbaar. Er werd dus ten onrechte een prijs van 1000$ uitgereikt voor de oplossing!