Sangaku 6 | Wiskunde is leuk

Antwoord

We zien een regelmatige zeshoek. Veronderstel dat de lengte van een zijde gelijk is aan 1. Zoek de afstand van A tot H.
We berekenen eerst 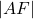$|AF|$ door gebruik te maken van de cosinusregel in driehoek AGF ( gelijkbenige driehoek met opstaande zijden gelijk aan 1 en een tophoek van $120^\circ$ . We vinden : $|AF|=\sqrt{3}$ .
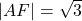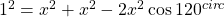We berekenen nu $|FH|$ in driehoek FEH. weer de cosinusregel : $1^2=x^2+x^2-2x^2\cos 120^÷circ$ . Hieruit volgt: $|AF|=\frac{1}{\sqrt{3}}$ .
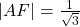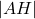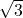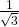Tenslotte berekenen we $|AH|$ in driehoek AHF. Cosinusregel met zijden $\sqrt{3}$ en $\frac{1}{\sqrt{3}}$ en ingesloten hoek $60^\circ$ . Dit geeft: $|AH|=\sqrt{\frac{7}{3}}$ .